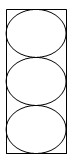
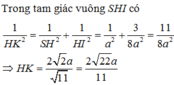Cho hình chóp Sabcd,ABCD là hình vuông,SAB cân tại S,H là trung điểm AB.CM SH vuông góc(ABCD)

Những câu hỏi liên quan
Cho hình chóp SABCD đáy ABCD là hình vuông cạch a SAB là tam giác đều và vuông góc (ABCD) .Gọi H là trung điểm AB a, Chứng minh SH vuông góc với (ABCD) b, chứng minh tam giác SBC vuông cân c, gọi I là trung điểm chứng minh SC vuông góc với DI
Cho hình chóp SABCD đáy là hình vuông cạnh 2a, (SAB) vuông góc (ABCD), tam giác SAB vuông cân tại A. Gọi H là trung điểm của AB. Tính góc giữa a) SB và (ABCD) b)SC và (ABCD)
\(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(ABCD\right)=AB\\SA\perp AB\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\widehat{SBA}=45^0\) (do SAB vuông cân tại A)
b.
\(\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=2a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{SC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SCA}\approx35^015'\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết
SH
a
,
CH
3
a
.
Tính khoảng cách giữa hai đường thẳng SD và CH. A.
14
a
2
B.
2...
Đọc tiếp
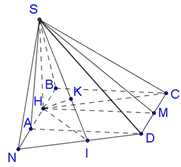
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH = a , CH = 3 a . Tính khoảng cách giữa hai đường thẳng SD và CH.
A. 14 a 2
B. 2 15 a 3
C. 2 22 a 11
D. 2 18 a 3
Đáp án C
Trong mặt phẳng (ABCD), kẻ DN//CH, dễ thấy AN = AH = HB = SH = a .

Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH a, CH
a
3
. Tính khoảng cách giữa hai đường thẳng SD và CH
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH = a, CH= a 3 . Tính khoảng cách giữa hai đường thẳng SD và CH
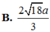
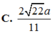
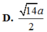
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH a, CH
3
a. Tính khoảng cách giữa hai đường thẳng SD và CH A.
2
15
a
3
B....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH = a, CH= 3 a. Tính khoảng cách giữa hai đường thẳng SD và CH
A. 2 15 a 3
B. 2 18 a 3
C. 2 22 a 11
D. 14 a 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, tam giác SAB cân tại S. SA=SB=2a, (SAB) \(\perp\) (ABCD)
a, Tính (SD,(ABCD))
b, (SH, (SCD)) với H là trung điểm của
c, (SC, (SAB))
d, (SA, (SBC))
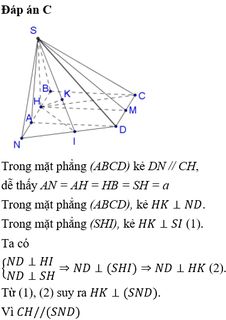
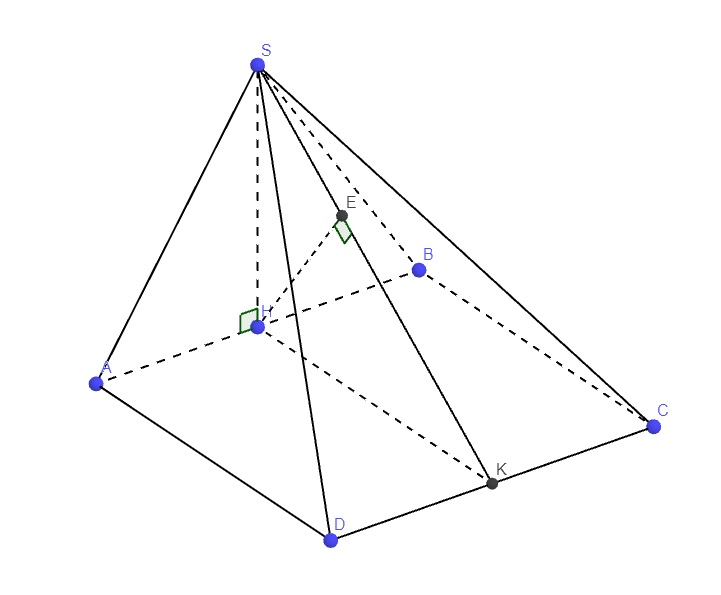
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng ABCD trùng với trung điểmH của cạnh AB. CHo SH=a√3/3. Gọi K là trung điểm CD
a) CM : (SAD)⊥(SAB)
b) Gọi α là góc giữa SM và (ABCD) . Xác định và tính tan α
c)Xác định và tính góc giữa 2 mặt phẳng (ABCD) và (SCD)
d) Tính khoảng cách từ H đến (SCD)
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
M là điểm nào nhỉ?
c.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\HK\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHK\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SCD) và (ABCD)
\(HK=AD=a\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SKH}=30^0\)
d.
Từ H kẻ \(HE\perp SK\) (E thuộc SK)
\(CD\perp\left(SHK\right)\) theo cmt \(\Rightarrow CD\perp HE\)
\(\Rightarrow HE\perp\left(SCD\right)\Rightarrow HE=d\left(H;\left(SCD\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}\Rightarrow HE=\dfrac{a}{2}\)
Đúng 1
Bình luận (0)
cho hình chóp SABCD đáy là hình vuông cạnh a, tam giác SAB cân tại S. (SAB) vuông góc với (ABCD) biết (SCD) tạo với đáy 1 góc 30°. Tính thể tích SABCD
Cho hình chóp SABCD có đáy là hình chữ nhật, AB2a, BCa. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD,
S
H
a
3
2
. Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD A.
4
πa
2
3
B.
16
πa...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình chữ nhật, AB=2a, BC=a. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD, S H = a 3 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD
A. 4 πa 2 3
B. 16 πa 2 3
C. 16 πa 2 3
D. 4 πa 3 3