Chứng minh rằng nếu \(A\subset B,B\subset D\) thì A \(\subset\) D

Những câu hỏi liên quan
chứng minh rằng nếu A \(\subset\) B ; B \(\subset\) D thì A\(\subset\) D
theo bài ra ta có:
A⊂B
B⊂D
=>A⊂D
tick hộ mik nha!
Đúng 0
Bình luận (0)
cái này thì hiển nhiên đúng rồi chứng minh làm gì nữa :)
Đúng 0
Bình luận (0)
Chứng minh rằng: Nếu \(A\subset C\) và \(B\subset C\) thì (\(A\cup B\))\(\subset C\)
a. Cho \(A\subset C\) và \(B\subset D\), chứng minh rằng \(\left(A\cup B\right)\subset\left(C\cup D\right)\)
b. Chứng minh rằng A\ \(\left(B\cap C\right)=\left(A\B\right)\cup\left(A\C\right)\)
c. Chứng minh rằng A\ \(\left(B\cup C\right)=\left(A\B\right)\cap\left(A\C\right)\)
Chứng minh rằng A\(\subset\)B ,mà B \(\subset\) C vậy A\(\subset\)C
Vì: \(a=b;b=c\Rightarrow a=c\)(tích chất bắt cầu)
\(\Rightarrow A\subset B;B\subset C\Rightarrow A\subset C\)
tíc mình nha
Đúng 0
Bình luận (0)
Chứng minh bằng hình vẽ :
Vòng tròn A nằm trong vòng tròn B,vòng tròn B nằm trong vòng tròn C nên vòng tròn A nằm trong vòng tròn C,suy ra đpcm.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh nếu A \(\subset\) B và B \(\subset\) A thì A = B
\(A\subset B\Rightarrow\)tất cả các phần tử của A đều có trong tập hợp B
\(B\subset A\Rightarrow\)tất cả các phần tử của B đều có trong tập hợp A
=>A=B
=>đpcm
Đúng 0
Bình luận (0)
Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)
Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
Tham khảo:
+) Biểu diễn: \(A \subset B\)
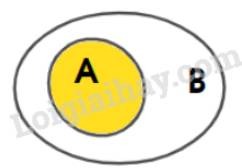
+) Sau đó, biểu diễn: \(B \subset C\)

Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)
Đúng 0
Bình luận (0)
[1] Cho tập hợp A = { 1; a; b }. Chọn khằng định sai:
A. \(\varnothing\subset A\) B. \(A\subset A\) C. \(1\subset A\) D. \(\left\{a;b\right\}\) \(\subset A\)
Ta có:
\(A=\left\{1;a;b\right\}\)
Xét:
A. \(\varnothing\subset A\) (đúng)
B. \(A\subset A\) (đúng)
C. \(1\subset A\) (sai)
D. \(\left\{a,b\right\}\subset A\) (đúng)
⇒ Chọn C
Đúng 2
Bình luận (0)
Cmr : A \(\subset\)B ; B \(\subset\)D Vậy thì : A\(\subset\)D
A\(\subset B\)=>các phần tử của tập hợp A thuộc tập hợp B
\(B\subset D\)=>các phần tử của tập hợp B thuộc tập hợp D
=>các phần tử của tập A thuộc tập hợp D
=>\(A\subset D\)
=>ĐPCM
Đúng 0
Bình luận (0)
Cho A,B,C là ba tập hợp . Mệnh đề nào sau đây là sai?
A. \(A\subset B\Rightarrow A\cap B\subset B\cap C\)
B. \(A\subset B=C\A\subset C\B\)
C. \(A\subset B\Rightarrow A\cup C\subset B\cup C\)
D. \(A\subset B,B\subset C\Rightarrow A\subset C\)
Mệnh đề A sai
Phản ví dụ: vì C bất kì nên \(B\cap C\) có thể bằng rỗng, mà \(A\cap B=A\) nên nếu \(A\ne\varnothing\) thì \(A\cap B\) không phải con của \(B\cap C\)























