\(\Leftrightarrow2cos^2x-1+2cosx-\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)=0\)

\(\Leftrightarrow2cos^2x+\dfrac{5}{2}cosx-\dfrac{3}{2}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{-5+\sqrt{73}}{8}\\cosx=\dfrac{-5-\sqrt{73}}{8}\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow x=\pm arccos\left(\dfrac{-5+\sqrt{73}}{8}\right)+k2\pi\)

1a.

Đặt \(5x+6=u\)

\(cos2u+4\sqrt{2}sinu-4=0\)

\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)

\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)

1b.

Đặt \(2x+1=u\)

\(cos2u+3sinu=2\)

\(\Leftrightarrow1-2sin^2u+3sinu=2\)

\(\Leftrightarrow2sin^2u-3sinu+1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)

2a.

\(cos^2x-sin^2x+sin^2x+2cosx+1=0\)

\(\Leftrightarrow cos^2x+2cosx+1=0\)

\(\Leftrightarrow\left(cosx+1\right)^2=0\)

\(\Leftrightarrow cosx=-1\)

\(\Leftrightarrow x=\pi+k2\pi\)

Đáp án A

Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.

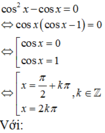
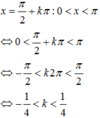
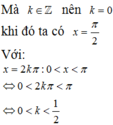
Mà k ∈ ℤ  nên không có giá trị k nào thỏa mãn.

Sai lầm và chú ý: Đối với những bài toán giải phương trình lượng giác thỏa mãn điều kiện cho trước, ta cần tìm được x sau đó cho x thỏa mãn điều kiện đầu bài và cô lập được k khi đó ta sẽ tìm được giá trị nguyên k thỏa mãn và sẽ tìm đc x.

Các bước biến đổi. Bạn tự tìm kết quả nhé!

1) \(\left(\sin x-\cos x\right)\left(\cos^2x+\cos x.\sin x+\sin^2x\right)+\cos^2x-\sin^2x=0\)

<=> \(\left(\sin x-\cos x\right)\left(1+\cos x.\sin x\right)+\left(\cos x-\sin x\right)\left(\cos x+\sin x\right)=0\)

<=> \(\left(\sin x-\cos x\right)\left(\cos x+1\right)\left(\sin x+1\right)=0\)

2) \(\left(\sin^3x-2\sin^5x\right)-\left(2\cos^5x-\cos^3x\right)=0\)

<=> \(\sin^3x\left(1-2\sin^2x\right)-\cos^3x\left(2\cos^2x-1\right)=0\)

<=> \(\sin^3x.\cos2x-\cos^3x.\cos2x=0\)

<=> \(\cos2x\left(\sin^3x-\cos^3x\right)=0\)

3) ĐK: x\(\ne\frac{\pi}{2}+k\pi\)

\(\cos x\left(3.\tan x+2\right)-\left(3\tan x+2\right)=0\)

<=> \(\left(\cos x-1\right)\left(3.\tan x+2\right)=0\)