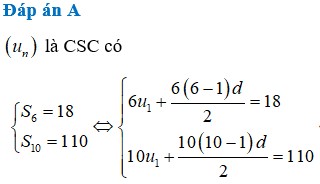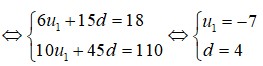Tìm csc có 6 số hạng, biết rằng tổng của 5 số hạng đầu = 31 và tổng của 5 số hạng sau = 62.

Những câu hỏi liên quan
Tìm cấp số nhân có 6 số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62 ?
Giả sử có cấp số nhân: u1, u2, u3, u4, u5,u6.
Theo giả thiết ta có:
u1 + u2 + u3 + u4 + u5 = 31. (1)
và u2 + u3 + u4 + u5 + u6 = 62. (2)
Nhân hai vế của (1) với q, ta được: q.u1 + q.u2 + q.u3 +q. u4 +q. u5 = 31.q
hay u2 + u3 + u4 + u5 + u6 = 31q
Suy ra 62 = 31.q hay q = 2.
Ta có S5 = 31 = 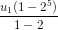 nên suy ra u1 = 1.
nên suy ra u1 = 1.
Vậy ta có cấp số nhân 1, 2, 4, 8, 16, 32.
Đúng 0
Bình luận (0)
Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.
Gọi cấp số nhân (un) cần tìm có công bội q, số hạng đầu tiên u1.
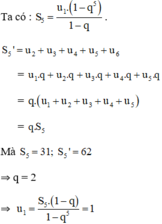
Vậy CSN (un) là: 1; 2; 4; 8; 16; 32.
Đúng 0
Bình luận (0)
Dãy số Tribonacci Sequence là dãy số mà kể từ số hạng thứ tư, mỗisố hạng đều bằng tổng của ba số hạng đứng liền trước. Ví dụ nếu ba sốhạng đầu tiên là 5, 6, 7 thì số hạng tiếp theo là 5 + 6 + 7 18, số thứ năm là6 + 7 + 18 31. Biết rằng năm số đầu tiên của dãy số Tribonacci Sequencelà P, Q, 86, 158 và 291. Hãy tìm giá trị của P
Đọc tiếp
Dãy số Tribonacci Sequence là dãy số mà kể từ số hạng thứ tư, mỗi
số hạng đều bằng tổng của ba số hạng đứng liền trước. Ví dụ nếu ba số
hạng đầu tiên là 5, 6, 7 thì số hạng tiếp theo là 5 + 6 + 7 = 18, số thứ năm là
6 + 7 + 18 = 31. Biết rằng năm số đầu tiên của dãy số Tribonacci Sequence
là P, Q, 86, 158 và 291. Hãy tìm giá trị của P
mọi người làm nhanh giúp mình nhé mình cần gấp đấy
Đúng 0
Bình luận (0)
Có bao nhiêu cấp số nhân có 5 số hạng? Biết rằng tổng 5 số hạng đó là 31 và tích của chúng là 1024.
A. 2
B. 3
C. 4
D. 1
Đáp án C
Xét 5 số hạng u 1 , u 2 , u 3 , u 4 , u 5 của cấp số nhân và công bội q
Theo bài ra, ta có:
∑ k = 1 5 u k = 31 ∏ k = 1 5 u k = 1024 ⇔ u 1 1 − q 5 1 − q = 31 u 1 5 . q 10 = 4 ⇒ 4 q 2 . 1 − q 5 1 − q = 31 *
Phương trình (*) có 4 nghiệm q phân biệt. Vậy có 4 cấp số nhân cần tìm
Đúng 0
Bình luận (0)
cho csc (un) tổng ba số hạng đầu tiên =-6 và tổng các bình phương của chúng = 30. hãy tìm csc
Gọi số hạng đầu tiên là a, công sai là d. 3 số hạng đầu là a,a+d.a+2d
a+(a+d)+(a+2d)=3a+3d=-6 nên d=-a-2
Suy ra 3 số hạng đầu là a, -2, -a-4
\(a^2+(-2)^2+(-a-4)^2=2a^2+8a+20=30\)
nên a=1,d=-3 hoặc a=-5,d=3
Đúng 0
Bình luận (0)
Một phép cộng có tổng của số hạng thứ nhất, và số hang thứ hai và tổng là 234. Tìm hai số hạng của tổng biết rằng số hạng thứ nhất bằng 4/5 số hạng thứ hai
tổng số phần là :4+5 =9 số thứ nhất là :234:9.4=104 số thứ 2 là : 234-104=130 k mk nha
Đúng 0
Bình luận (0)
Cho một cấp số cộng, biết rằng tổng của sáu số hạng đầu bẳng 18 và tổng của mười số hạng đầu bằng 110. Tìm số hạng tổng quát
u
n
A.
u
n
-
11
+
4
n
B.
u
n
11
+
4
n
C.
u
n
-
11
-
4
n...
Đọc tiếp
Cho một cấp số cộng, biết rằng tổng của sáu số hạng đầu bẳng 18 và tổng của mười số hạng đầu bằng 110. Tìm số hạng tổng quát u n
A. u n = - 11 + 4 n
B. u n = 11 + 4 n
C. u n = - 11 - 4 n
D. u n = 11 - 4 n
tìm 1 cấp số cộng có 5 số hạng ,biết tổng số hạng đầu với số hạng thứ 3 bằng 28 và tổng số hạng thứ 3 với số hạng cuối là 40
Gọi số đầu là x.
Cấp số cộng là q.
=> Số đầu, thứ 2. 3,4,5 là x,x+q,x+2q,x+3q,x+4q.
Tổng số 1 và 3 là x + (x+2q) = 28
Tổng số 3 và cuối là (x+2q)+(x+4q)=40.
Ta đã có 2 phương trình tạo thành 1 hệ phương trình.
Giải hệ tìm x và q.
Chúc em học tốt!
Đúng 1
Bình luận (0)
Tìm bốn số biết rằng ba số hạng đầu lập thành một cấp số nhân, ba số hạng sau lập thành một cấp số công. Tổng của hai số hạng đầu và cuối bằng 14, còn tổng của 2 số ở giữa là 12 ?
Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)
Đúng 0
Bình luận (0)