c) Để A nhận giá trị nguyên khi và chỉ khi:

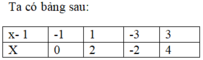
Kết hợp với điều kiện, tập hợp các giá trị của x nguyên để A nguyên là: {0; 2; -2; 4}.

đề bài ĐKXĐ như nào bạn tự xét gtri thỏa mãn nhé

\(P=\frac{x^2}{x-1}=\frac{x^2-x+x-1+1}{x-1}=\frac{x\left(x-1\right)+\left(x-1\right)+1}{x-1}=x+1+\frac{1}{x-1}\)

Vì x nguyên nên x + 1 nguyên

Để P nguyên thì 1/x-1 nguyên ( đến đây quá dễ rồi:)) )

Như trên ta có : \(P=x+1+\frac{1}{x-1}=\left[\left(x-1\right)+\frac{1}{x-1}\right]+2\)

Vì x > 1, áp dụng bất đẳng thức AM-GM ta có : 

\(P\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+2=4\). Đẳng thức xảy ra <=> x = 2

Vậy GTNN của P = 4 <=> x=2

a) ĐKXĐ: \(x\notin\left\{5;-5\right\}\)

b) Ta có: \(A=\dfrac{2x}{x^2-25}+\dfrac{5}{5-x}-\dfrac{1}{x+5}\)

\(=\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5}{x-5}-\dfrac{1}{x+5}\)

\(=\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}\)

\(=\dfrac{2x-5x-25-x+5}{\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{-4x-20}{\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{-4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{-4}{x-5}\)

Để A nguyên thì \(-4⋮x-5\)

\(\Leftrightarrow x-5\inƯ\left(-4\right)\)

\(\Leftrightarrow x-5\in\left\{1;-1;2;-2;4;-4\right\}\)

hay \(x\in\left\{6;4;7;3;9;1\right\}\)(nhận)

Vậy: Để A nguyên thì \(x\in\left\{6;4;7;3;9;1\right\}\)

a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)

Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên

\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên

\(\Rightarrow11⋮4x-5\)

Vì \(x\in Z\) nên \(4x-5\in Z\)

\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)

Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).

b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)

Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)

       4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)

Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất

\(\Rightarrow4-x=1\Rightarrow x=3\)

\(\Rightarrow A=\dfrac{5}{4-3}=5\)

Vậy MaxA = 5 tại x = 3

c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).

Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)

Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất

\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất

Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\) 

       x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)

Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất

\(\Rightarrow x-3=-1\Rightarrow x=2\)

\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)

Vậy MaxB = -6 tại x = 2.

a) Để M nhận giá trị nguyên thì \(8x+1⋮4x-1\)

\(\Leftrightarrow8x-2+3⋮4x-1\)

mà \(8x-2⋮4x-1\)

nên \(3⋮4x-1\)

\(\Leftrightarrow4x-1\inƯ\left(3\right)\)

\(\Leftrightarrow4x-1\in\left\{1;-1;3;-3\right\}\)

\(\Leftrightarrow4x\in\left\{2;0;4;-2\right\}\)

\(\Leftrightarrow x\in\left\{\dfrac{1}{2};0;1;-\dfrac{1}{2}\right\}\)

mà x là số nguyên

nên \(x\in\left\{0;1\right\}\)

Vậy: \(x\in\left\{0;1\right\}\)

\(\dfrac{3x+6}{x+1}\) \(\in\) Z \(\Leftrightarrow\) 3\(x\) + 6 \(⋮\) \(x\) + 1 \(\Leftrightarrow\) 3\(x\) + 3 + 3 \(⋮\) \(x\) + 1

                                              \(\Leftrightarrow\)                 3 \(⋮\) \(x+1\)

                                      \(x+1\) \(\in\) { -3; -1; 1; 3}

                                       \(x\)       \(\in\) { -4; -2; 0; 2}