trên đường thẳng (d) : x-y+2=0 , tìm điểm M cách đều 2 điểm E(0,4) và F(4,-9).

Những câu hỏi liên quan
trên đường thẳng (d) : x-y+2=0 , tìm điểm M cách đều 2 điểm E(0,4) và F(4,-9).
M cách đầu E và F =>M là trung điểm của EF
Gọi tọa độ điểm M là M(xM;yM)
=>\(x_M=\frac{x_E+x_F}{2}=\frac{0+4}{2}=2;y_M=\frac{y_E+y_F}{2}=\frac{4-9}{2}=-\frac{5}{2}\)
Vậy M(2;-5/2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
trên đường thẳng (d) : x-y+2=0 , tìm điểm M cách đều 2 điểm E(0,4) và F(-4,9).
trên đường thẳng (d) : x-y+2=0 , tìm điểm M cách đều 2 điểm E(0,4) và F(-4,9).
trung điểm H của EF là H( -2; 13/2)
trung trực của EF ; 5x+4y +c =0 qua H => 5.(-2) + 4 .13/2 + c =0 => c =-16
M là giao của (d') : 5x+4y -16 =0 và (d) => M(8/9 ; 26/9)
Đúng 0
Bình luận (0)
Đường thẳng (d) qua E(0,4) và F(4,-9) có dạng: y = ax + b. thay tọa độ E, F vào có:
{ 4 = a.0 + b
{ - 9 = a.4 + b
=> b = 4; a = -13/4
=> pt của (d) là : 13x + 4y - 16 = 0
M cách đều E, F nên thuộc đường thẳng trung trực (d') của EF. Gọi I là trung điểm EF có tọa độ của I là :
{ xi = (xE + xF)/2 = (0 + 4)/2 = 2
{ yi = (yE + yF)/2 = (4 + (-9))/2 = -5/2
(d') vuông góc (d) nên Pt của (d') có dạng 4x - 13y + c' = 0
(d') qua I(2,-5/2) nên : 4.2 - 13.(-5/2) + c' = 0 => c' = - 61/2
=> pt của (d') là : 8x - 26y - 61 = 0
M vừa thuộc delta, vừa thuộc (d') nên là nghiệm của hệ:
{ x - y +2 = 0
{ 8x - 26y - 61 = 0
Giải ra x = 41/18; y = 77/18
Vậy M(41/18; 77/18) là điểm cần tìm
Đúng 0
Bình luận (0)
trung trực của EF: 4(x+2) - 5(y- 13/2) =0 hay 4x - 5y +81/2=0
M là giao diểm cảu EF và d
=> \(\sum_{4x-5y=-\frac{81}{2}}^{x-y=-2}\)=> M (61/2 ; 65/2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
trên đường thẳng (d) : x-y+2=0 , tìm điểm M cách đều 2 điểm E(0,4) và F(-4,9).
6 vị trí tương đối của các cặp đường thẳng sau : a d1 : 14x+y+20 và d2 : x+4y+10+10 b d1 : d2: c d1 : d2 : 2x+4y-100 d d1 : x+y-20 và d2: 2x+y-30 7 Viết phương trình đường thẳng d đi qua M( 2;5) và cách đều hai điểm A(-1;2) , B(5;4) 8 Tìm trên đường thẳng ΔΔ : x-y+20 điểm M cách đều hai điểm E(0;4) , F(4;-9)9 Cho đường thẳng d: x-y0 và điểm M (2;1) a Viết phương trình đường thẳng đối xứng với d qua điểm M b Tìm hình chiếu của điểm M trên D .
Đọc tiếp
6> vị trí tương đối của các cặp đường thẳng sau :
a> d1 : 14x+y+2=0 và d2 : x+4y+10+1=0
b> d1 : 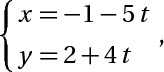 d2:
d2: 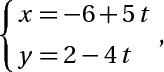
c> d1 : 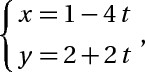 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
d> d1 : x+y-2=0 và d2: 2x+y-3=0
7> Viết phương trình đường thẳng d đi qua M( 2;5) và cách đều hai điểm A(-1;2) , B(5;4)
8 Tìm trên đường thẳng ΔΔ : x-y+2=0 điểm M cách đều hai điểm E(0;4) , F(4;-9)
9> Cho đường thẳng d: x-y=0 và điểm M (2;1)
a> Viết phương trình đường thẳng đối xứng với d qua điểm M
b> Tìm hình chiếu của điểm M trên D .
Trong mặt phẳng toạ độ Oxy, cho đường thẳng d: x=2-t; y= 3+2t và điểm A(2,7) Tìm trên d điểm E sao cho OE=√2 Tìm trên d điểm M cách đường thẳng d2: 3x+4y-1=0 một khoảng bằng 1 Tìm trên d điểm N sao cho AN = 2 ON
Trong mặt phẳng Oxy, cho điểm Fleft( {0;frac{1}{2}} right), đường thẳng Delta :y + frac{1}{2} 0 và điểm M(x;y). Để tìm hệ thức giữa x và y sao cho M cách đều F và Delta , một học sinh đã làm như sau:+) Tính MF và MH (với H là hình chiếu của M trên Delta ):MF sqrt {{x^2} + {{left( {y - frac{1}{2}} right)}^2}} ,MH dleft( {M,Delta } right) left| {y + frac{1}{2}} right|+) Điều kiện để M cách đều F và Delta :begin{array}{l}MF dleft( {M,Delta } right) Leftrightarrow sqrt {{x^2} + {{left( {y - f...
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm \(F\left( {0;\frac{1}{2}} \right)\), đường thẳng \(\Delta :y + \frac{1}{2} = 0\) và điểm \(M(x;y)\). Để tìm hệ thức giữa x và y sao cho \(M\) cách đều F và \(\Delta \), một học sinh đã làm như sau:
+) Tính MF và MH (với H là hình chiếu của M trên \(\Delta \)):
\(MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|\)
+) Điều kiện để M cách đều F và \(\Delta \):
\(\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}\)
Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.
Đúng 0
Bình luận (0)
Cho 3 đường thẳng (d1) x=1-2t y=1+t, (d2): 3x+4y-4=0, (d3): 4x-3y+2=0 . Tìm điểm M nằm trên (d1) cách đều (d2) và d3
M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)
Đúng 1
Bình luận (0)
Điểm E(4;5;5), mặt phẳng (P): x-2y+2z+60 và đường thẳng
d
:
x
+
1
2
y
-
3
-
1
z
-
2
1
. Tìm tọa độ điểm M có hoành độ nhỏ hơn 2 nằm trên đường thẳng d có khoảng cách...
Đọc tiếp
Điểm E(4;5;5), mặt phẳng (P): x-2y+2z+6=0 và đường thẳng d : x + 1 2 = y - 3 - 1 = z - 2 1 . Tìm tọa độ điểm M có hoành độ nhỏ hơn 2 nằm trên đường thẳng d có khoảng cách từ M tới mặt phẳng (P) bằng EM.
![]()
![]()
![]()
![]()



















