một túi đụng 4 viên bi đỏ, 3 viên bi trắng và 5 viên bi vàng. chọn ngẫu nhiên 3 viên bi. tính xs để 3 viên bi đc chọn có đủ cả 3 màu.

Những câu hỏi liên quan
Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi.
b) Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là
A. 1/14
B. 45/182
C. 1/90
D. 1/364
b. Gọi A là biến cố:” 3 bi xảy ra có cả 3 màu đỏ, xanh. Vàng” thì
![]()
Chọn B
Đúng 0
Bình luận (0)
một hộp đựng 3 viên bi màu xanh 5 viên bi màu đỏ và 6 viên bi màu vàng. chọn ngẫu nhiên 5 viên bi. Tính xác suất để 5 viên bi được chọn đủ 3 màu và có ít nhất 2 viên bi xanh
Không gian mẫu: \(C_{14}^5\)
Các cách chọn thỏa mãn gồm có: (1 đỏ 1 vàng 3 xanh), (2 đỏ 1 vàng 2 xanh), (1 đỏ 2 vàng 2 xanh)
Số cách: \(C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2\)
Xác suất: \(P=\dfrac{C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2}{C_{14}^5}=...\)
Đúng 0
Bình luận (0)
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ 3 màu và số bi đỏ bằng số bi vàng. A.
313
408
B.
95
408
C.
5
102
D.
25
136
Đọc tiếp
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ 3 màu và số bi đỏ bằng số bi vàng.
A. 313 408
B. 95 408
C. 5 102
D. 25 136
Đáp án B
Có các cách chọn sau:
+) 1 bi đỏ, 1 bi vàng, 3 bi xanh, suy ra có C 6 1 C 7 1 C 5 3 = 420 cách.
+) 2 bi đỏ, 2 bi vàng, 1 bi xanh, suy ra có C 6 2 C 7 2 C 5 1 = 1575 cách.
Suy ra xác suất bằng 420 + 1575 C 18 5 = 95 408 .
Đúng 0
Bình luận (0)
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ 3 màu và số bi đỏ bằng số bi vàng.
A. 313 408
B. 95 408
C. 5 102
D. 25 136
Một hộp có 12 viên bi khác nhau gồm : 3 viên bi màu đỏ, 4 viên bi màu trắng, 5 viên bi màu vàng. Chọn ngẫu nhiên 4 viên bi từ hộp đó. Số cách chọn ra 4 viên bi không đủ ba màu là.
TH1: 4 viên được lấy chỉ gồm 2 màu đỏ và trắng.
\(\Rightarrow\) Có \(C^4_7\) cách chọn.
TH2: 4 viên được lấy chỉ gồm 2 màu đỏ và vàng.
\(\Rightarrow\) Có \(C^4_8\) cách chọn.
TH3: 4 viên được lấy chỉ gồm 2 màu trắng và vàng.
\(\Rightarrow\) Có \(C^4_9\) cách chọn.
TH2 và TH3 đã bao gồm TH lấy 4 viên chỉ có màu trắng và 4 viên chỉ có màu vàng.
\(\Rightarrow\) Có \(C^4_7+C^4_8+C^4_9-C^4_4-C^4_5=225\) cách chọn ra 4 viên bi không đủ ba màu.
Đúng 1
Bình luận (0)
Có hai chiếc túi, chiếc túi đầu tiên đựng 4 viên bi màu xanh và 3 viên bi màu vàng, chiếc túi còn lại chứa 3 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên một viên bi.a) Tính xác suất để lấy ra được một viên bi xanhb) Nếu một viên bi xanh được lấy ra, tính xác suất mà nó được lấy ra từ chiếc túi thứ nhất.
Đọc tiếp
Có hai chiếc túi, chiếc túi đầu tiên đựng 4 viên bi màu xanh và 3 viên bi màu vàng, chiếc túi còn lại chứa 3 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên một viên bi.
a) Tính xác suất để lấy ra được một viên bi xanh
b) Nếu một viên bi xanh được lấy ra, tính xác suất mà nó được lấy ra từ chiếc túi thứ nhất.
a: n(omega)=4+3+3+5=15
n(xanh)=4+3=7
=>P=7/15
b: P=7/15*4/7=4/15
Đúng 0
Bình luận (0)
Một túi đựng 10 bi đỏ và 5 bi xanh, chọn ngẫu nhiên 3 viên bi. Tính số cách để chọn được A) 3 viên bi xanh B) có đúng 1 viên bi màu đỏ C) có ít nhất 1 viên bi màu xanh
Một túi có 10 viên bi trong đó có 7 viên bi đỏ và 3 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Tính xác suất để trong 3 viên bi đó có ít nhất 1 viên bi vàng.
A. 3/2
B. 2
C. 17/24
D. 19/26
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng. A.
95
408
.
B.
5
102
.
C.
25
136
.
D.
313
4...
Đọc tiếp
Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.
A. 95 408 .
B. 5 102 .
C. 25 136 .
D. 313 408 .
Đáp án A
Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.Suy ra số phần tử của không gian mẫu là Ω = C 18 5 = 8568 .
Gọi A là biến cố 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng . Ta có các trường hợp thuận lợi cho biến cố A là:
● TH1: Chọn 1 bi đỏ, 1 bi vàng và 3 bi xanh nên có C 6 1 . C 7 1 . C 5 3 cách.
● TH2: Chọn 2 bi đỏ, 2 bi vàng và 1 bi xanh nên có C 6 2 . C 7 2 . C 5 1 cách.
Suy ra số phần tử của biến cố A là
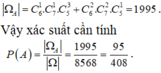
Đúng 0
Bình luận (0)













