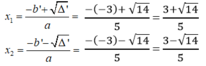Giải các pt sau bằng công thức nghiệm
5x2 - 6x + 1 = 0
Cho các PT sau: 3x2-4x+1=0; -x2+6x-5=0 a, Giải các PT trên bằng công thức nghiệm hoặc công thức nghiệm thu gọn.
a: 3x^2-4x+1=0
a=3; b=-4; c=1
Vì a+b+c=0 nên phương trình có hai nghiệm là:
x1=1 và x2=c/a=1/3
b: -x^2+6x-5=0
=>x^2-6x+5=0
a=1; b=-6; c=5
Vì a+b+c=0 nên phương trình có hai nghiệm là;
x1=1; x2=5/1=5
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
(2) giải các pt sau bằng công thức nghiệm (hoặc công thức nghiện thu gọn)
1) \(x^2-11x+30=0\)
2) \(x^2-x-20=0\)
3) \(x^2+14x+24=0\)
4) \(3x^2+8x-2=0\)
giúp mk vs ạ mk đang cần gấp
\(1,\Delta=\left(-11\right)^2-4\cdot30=1\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11-1}{2}=5\\x=\dfrac{11+1}{2}=6\end{matrix}\right.\\ 2,\Delta=\left(-1\right)^2-4\left(-20\right)=81\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{81}}{2}=-4\\x=\dfrac{1+\sqrt{81}}{2}=5\end{matrix}\right.\\ 3,\Delta=14^2-4\cdot24=100\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-14-\sqrt{100}}{2}=-12\\x=\dfrac{-14+\sqrt{100}}{2}=-2\end{matrix}\right.\\ 4,\Delta=8^2-4\left(-2\right)3=88\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-8-\sqrt{88}}{6}=\dfrac{-4+\sqrt{22}}{3}\\x=\dfrac{-8+\sqrt{88}}{6}=\dfrac{-4-\sqrt{22}}{3}\end{matrix}\right.\)
1) Δ = (-11)2 -4.1.30 = 1 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta}\)=1.
x1 = \(\dfrac{-\left(-11\right)+1}{2.1}\) = 6, x2 = \(\dfrac{-\left(-11\right)-1}{2.1}\) = 5.
2) Δ = (-1)2 -4.1.(-20) = 81 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta}\)=9.
x1 = \(\dfrac{-\left(-1\right)+9}{2.1}\) = 5, x2 = \(\dfrac{-\left(-1\right)-9}{2.1}\) = -4.
3) Δ' = 72 -1.24 = 25 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta'}\)=5.
x1 = \(\dfrac{-7+5}{1}\) = -2, x2 = \(\dfrac{-7-5}{1}\) = -12.
4) Δ' = 42 -3.(-2) = 22 > 0 ⇒ Phương trình đã cho có hai nghiệm phân biệt, \(\sqrt{\Delta'}\)=\(\sqrt{22}\).
x1 = \(\dfrac{-4+\sqrt{22}}{3}\), x2 = \(\dfrac{-4-\sqrt{22}}{3}\).
2. Xác định các hệ số a,b,c Tính biệt thức từ đó áp dụng công thức nghiệm để giải các pt sau:
a. \(3x^2-4x+1=0\)
b. \(-4x^2+4x+1=0\)
d. \(x^2-\sqrt{8}x+2=0\)
e. \(x^2-6x+5=0\)
a) 3x² - 4x + 1 = 0
a = 3; b = -4; c = 1
∆ = b² - 4ac = (-4)² - 4.3.1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = [-(-4) + 2]/(2.3) = 1
x₂ = (-b - √∆)/2a = [-(-4) - 2]/(2.3) = 1/3
Vậy S = {1/3; 1}
b) -4x² + 4x + 1 = 0
a = -4; b = 4; c = 1
∆ = b² - 4ac = 4² - 4.(-4).1 = 32 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = (-4 + 4√2)/[2.(-4)] = (1 - √2)/2
x₂ = (-b - √∆)/2a = (-4 - 4√2)/[2.(-4)] = (1 + √2)/2
Vậy S = {(1 - √2)/2; (1 + √2)/2}
d) x² - 8x + 2 = 0
a = 1; b = -√8; c = 2
∆ = b² - 4ac = 8 - 8 = 0
Phương trình có nghiệm kép:
x₁ = x₂ = -b/2a = √8/2 = √2
Vậy S = {√2}
e) x² - 6x + 5 = 0
a = 1; b = -6; c = 5
∆ = b² - 4ac = 36 - 20 = 16 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = (6 + 4)/2 = 5
x₂ = (-b - √∆)/2a = (6 - 4)/2 = 1
Vậy S = {1; 5}
giải pt sau bằng công thức nghiệm
x^2 + 4x + 4 = 0
ta có :Δ' = 22 - 2.4 = 4 - 8 = - 4
==> pt trên vô nghiệm
Δ' = \(2^2 - 1.4 = 0\)
⇒ Phương trình đã cho có nghiệm kép
\(x_1 = x_2 = -2 \)
Vậy...
Giải các phương trình sau bằng hai cách (phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được: 3 5 x 2 + 6x = 0
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
5x2 – 6x + 1 = 0
Phương trình bậc hai 5x2 – 6x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ’ = (b’)2 – ac = (-3)2 – 5.1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
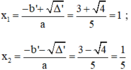
Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn: 9 x 2 + 6x + 1 = 0
Phương trình 9 x 2 +6x+1 =0 có hệ số a=9,b’=3,c=1
Ta có: ∆ ’ = b ' 2 – ac = 3 2 -9.1 = 9 - 9 = 0
Phương trình có nghiệm kép:
x 1 = x 2 = -b'/a =-3/9 =-1/3
Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn: 5 x 2 – 6x -1 = 0
Phương trình 5 x 2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: ∆ ’ = b ' 2 – ac = - 3 2 -5.(-1) = 9 + 5 = 14 > 0
∆ ' = 14
Phương trình có hai nghiệm phân biệt :