Phân tích thành nhân tử: 3 + 2x (x < 0)

Những câu hỏi liên quan
Phân tích thành nhân tử: 3 + 2x (x < 0)
\(2x+3=2\left(x+\dfrac{3}{2}\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử : 2x^4-x^3+2x^2+3x-2=0
Ta có
2x^4-x^3+2x^2+3x-2
=x^3(2x-1)+(2x^2-x)+(4x-2)
=x^3(2x-1)+x(2x-1)+2(2x-1)
=(x^3+x+2)(2x-1)
Đúng 0
Bình luận (0)
phân tích vế trái thành nhân tử, giải phương trình sau: 2x(x – 3) + 5(x – 3) = 0
2x(x – 3) + 5(x – 3) = 0
⇔ (2x + 5)(x – 3) = 0
⇔ 2x + 5 = 0 hoặc x – 3 = 0
+ 2x + 5 = 0 ⇔2x = -5 ⇔ x = -5/2
+ x – 3 = 0 ⇔x = 3.
Vậy phương trình có tập nghiệm 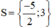
Đúng 0
Bình luận (0)
Phân tích thành nhân tử
(x-3)^2-5(x-2)+5=0
(2x-1)^2-3(x-2)(x+2)-25=0
\(\left(x-3\right)^2-5\left(x-2\right)+5=0\\ \Leftrightarrow x^2-6x+9-5x+10+5=0\\ \Leftrightarrow x^2-11x+24=0\\ \Leftrightarrow\left(x-8\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
\(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\\ \Leftrightarrow4x^2-4x+1-3\left(x^2-4\right)-25=0\\ \Leftrightarrow4x^2-4x-24-3x^2+12=0\\ \Leftrightarrow x^2-4x-12=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a: Ta có: \(\left(x-3\right)^2-5\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-6x+9-5x+10+5=0\)
\(\Leftrightarrow x^2-11x+24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
b: Ta có: \(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\)
\(\Leftrightarrow4x^2-4x+1-3x^2+12-25=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
x^3 + 2x^2 + 2x + 1 = 0
Sử dụng phương pháp phân tích thành nhân tử
Ta có : x3 + 2x2 + 2x + 1 = 0
<=> x3 + 2x2.1 + 2.12.x + 13 = 0
<=> (x + 1)3 = 0
=> x + 1 = 0
=> x = -1
Đúng 0
Bình luận (0)
\(x^3+2x^2+2x+1=0\)
\(x^3+x^2+x^2+x+x+1=0\)
\(x^2\left(x+1\right)+x\left(x+1\right)+x+1=0\)
\(\left(x+1\right)\left(x^2+x+1\right)=0\)
Vì \(x^2+x+1=x^2+2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}\)
\(=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow x+1=0\)
\(\Rightarrow x=-1\)
Đúng 0
Bình luận (0)
x^3 + 2x^2 + 2x +1=0
suy ra:x(x^2 + 2x +1) + 2X =0
suy ra:x=0 hoặc (x+1)^2 =0 hoặc 2x=0
suy ra:x=0 hoặc x = -1 hoặc x=0
vậy x=0 hoặc x =-1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
10/ tìm x ( áp dụng kiến thức phân tích đa thức thành nhân tử) d,2x^3+3x^2+3+2x =0
Ta có: \(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow x^2\left(2x+3\right)+\left(2x+3\right)=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
Đa thức x^3 - 2x^2 + x - xy^2 được phân tích thành nhân tử
Đa thức x^3 + 3x^2y +3xy^2 + y^3 được phân tích thành nhân tử là
Đa thức 4x(2y-z)+7y(2y-z) được phân tích thành nhân tử là:
Đa thức x^2+4x+4 được phân tích thành nhân tử là
Tìm x biết x(x-2)-x+2
\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Phân tích vế trái thành nhân tử, giải phương trình sau: (x2 – 4) + (x – 2)(3 – 2x) = 0
(x2 – 4) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0
⇔ (x – 2)(5 – x) = 0
⇔ x – 2 = 0 hoặc 5 – x = 0
+ x – 2 = 0 ⇔ x = 2
+ 5 – x = 0 ⇔ x = 5.
Vậy tập nghiệm của phương trình là S = {2; 5}.
Đúng 0
Bình luận (0)
Phân tích thành nhân tử: x * sqrt(x) + 2x + sqrt(x) +2(với x>0)
\(x\sqrt{x}+2x+\sqrt{x}+2\left(x>0\right)\)
\(=\left(x\sqrt{x}+\sqrt{x}\right)+\left(2x+2\right)\)
\(=\sqrt{x}\left(x+1\right)+2\left(x+1\right)\)
\(=\left(\sqrt{x}+2\right)\left(x+1\right)\)
Đúng 2
Bình luận (0)























