Giúp mình với ạ, gấp lắm ạ😥😥

Những câu hỏi liên quan
Mọi người giúp mình câu ba với ạ, cần gấp lắm ạ!! 😥😥😥
Anh nghĩ với bài kiểm tra em nên tự làm nhé.
Đúng 1
Bình luận (1)
Giúp mình với ạ, mình cần gấp lắm😥😥
a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow1+2sinx.cosx=t^2\Rightarrow2sinx.cosx=t^2-1\)
Phương trình trở thành:
\(3t=2\left(t^2-1\right)\)
\(\Leftrightarrow2t^2-3t-2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2>\sqrt{2}\left(loại\right)\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(1+\dfrac{sinx}{cosx}=2\sqrt{2}sinx\)
\(\Rightarrow sinx+cosx=2\sqrt{2}sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\)
Đúng 0
Bình luận (0)
c.
\(\Leftrightarrow1+sinx+cosx+sinx.cosx=2\)
\(\Leftrightarrow sinx+cosx+sinx.cosx=1\)
Đặt \(sinx+cosx=t\in\left[-\sqrt[]{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t+\dfrac{t^2-1}{2}=1\)
\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mn giúp mình vời ạ, mình cần gấp lắm😥😥!!!
a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)
Đúng 1
Bình luận (0)
e.
\(B=\dfrac{\dfrac{3cosa}{sina}+\dfrac{2sina}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{3cos^2a+2sin^2a}{sin^2a+cos^2a}=3\left(1-sin^2a\right)+2sin^2a\)
\(=3-sin^2a=\dfrac{26}{9}\)
f.
\(C=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}=\dfrac{2tana+3}{tana+1}=\dfrac{7}{3}\)
g.
\(C=\dfrac{\dfrac{3sina}{sina}-\dfrac{4cosa}{sina}}{\dfrac{cosa}{sina}-\dfrac{2sina}{sina}}=\dfrac{3-4cota}{cota-2}=1+\sqrt{5}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em bài này với ạ, gấp lắm ạ😥
Giúp mình bài này đc không ạ, mình cần gấp lắm😥
1 Jill reminded John to do the washing up
2 The police ordered his men to search all the shops on that street
3 She blamed me for ignoring the notice about life-saving equipment
4 My aunt advised me not to argut with my father
5 Stella congratulated Jeff on having got an promotion at last
6 Kevin apoligized to Sarah for making her angry
7 The man warn his son to put down the gun
8 Ron denied being in the town on the night of the robbery
9 Ted promise to pay back the money at the end of that month
10 George encouraged Susan to send her story to the magazine
11 Natalie accused Tom of lying to her
Đúng 1
Bình luận (0)
Ai biết giải giúp em đề 3 với ạ gấp lắm ạ 😥
2:
a: pi/2<a<pi
=>cosa<0
sin^2a+cos^2a=1
=>cos^2a=1-4/9=5/9
=>cosa=-căn 5/3
cos2a=2*cos^2a-1=2*5/9-1=10/9-1=1/9
sin(2a-pi/6)
=sin2a*cospi/6-cos2a*sinpi/6
=2*sina*cosa*(căn 3/2)-1/9*1/2
\(=2\cdot\dfrac{2}{3}\cdot\dfrac{-\sqrt{5}}{3}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{1}{18}=\dfrac{-4\sqrt{15}-1}{18}\)
b; tan a=2
=>sin a=2*cosa
\(A=\dfrac{3\cdot\left(2\cdot cosa\right)^2-cos^2a+2}{5\cdot\left(2\cdot cosa\right)^2+3cosa\cdot2cosa}\)
\(=\dfrac{12\cdot cos^2a-cos^2a+2}{20cos^2a+6cos^2a}\)
\(=\dfrac{11cos^2a+2\left(4cos^2a+cos^2a\right)}{26cos^2a}=\dfrac{21}{26}\)
4:
a: (C): x^2+y^2-4x+2y-4=0
=>x^2-4x+4+y^2+2y+1=9
=>(x-2)^2+(y+1)^2=9
=>I(2;-1); R=3
b: Gọi (d) là phương trình cần tìm
(d)//4x+3y-1=0
=>(d): 4x+3y+c=0
I(2;-1);R=3
Theo đề, ta có: d(I;(d))=R=3
=>\(\dfrac{\left|4\cdot2+3\cdot\left(-1\right)+c\right|}{\sqrt{4^2+3^2}}=3\)
=>|c+5|=15
=>c=10 hoặc c=-20
Đúng 0
Bình luận (0)
Giúp mình bài này được không ạ? Mình đang cần gấp lắm😥😧
D C D B C C C D A
Sam puts up the decorations.
Five guests came to the party.
Molly and Sam play video games with their cousins
The family was celebrating too early. Dad's birthday was two months away.
relationship
celebration
married
golden
quietly
celebratory
refer
1. he dislike being called " the liar " => He dislike people..CALLING HIM THE LIAR.
2. The police are following the suspects => The suspects ..ARE BEING FOLLOWED BY THE POLICE.
3. She always expects to be admired by everybody => She always expects everybody..TO ADMIRE HER...
4. Someone stole his car two days ago => He had ..HIS CAR STOLEN BY SOMEONE TWO DAYS AGO..
Đúng 0
Bình luận (0)
Giúp em với ạ. Cần gấp 😥😥😥😥🙏🙏🙏🙏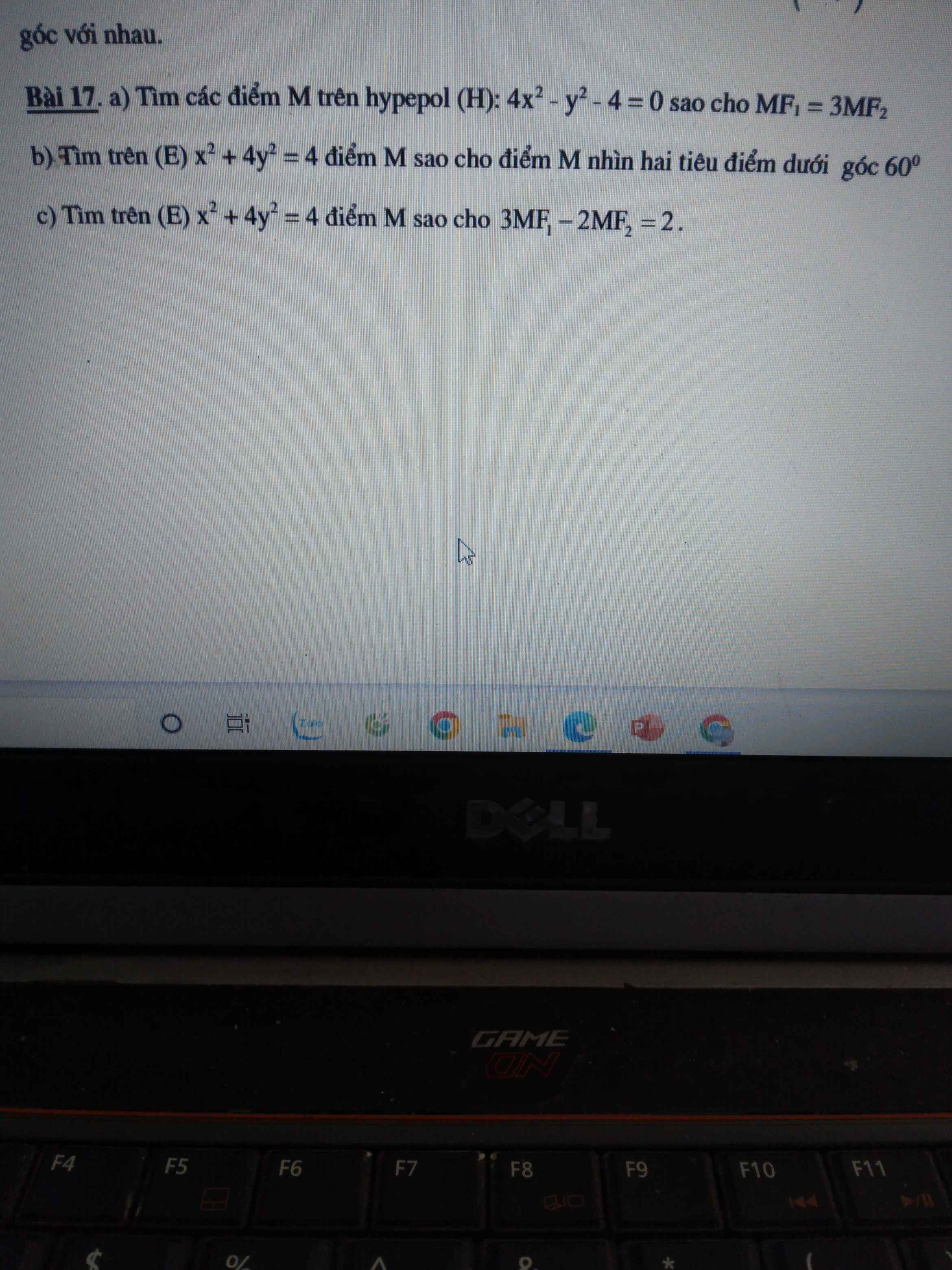
Giúp mình được không ạ? Bài này mình cần gấp😥😥
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì trên (E) \(\Rightarrow\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in\left(E'\right)\) với (E') là ảnh của (E) qua phép tịnh tiến nói trên
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{\left(x'-3\right)^2}{16}+\dfrac{\left(y'+2\right)^2}{9}=1\)
Hay pt (E') có dạng: \(\dfrac{\left(x-3\right)^2}{16}+\dfrac{\left(y+2\right)^2}{9}=1\)
Đúng 0
Bình luận (0)











