Bài 3. Cho tam giác đều ABC. Gọi D, E lần lượt là trung điểm của các cạnh AB và
AC.
a) Chứng minh: BDEC là hình thang cân có đáy nhỏ bằng cạnh bên.
b) Tính chu vi hình thang cân BDEC biết AB = 6cm.

Những câu hỏi liên quan
Cho ▲ABC cân tại A trên cạnh AB, AC lần lượt lấy 2 điểm D, E sao cho AD=AE.
a/ Chứng minh tứ giác BDEC là hình thang cân
b/ Cho góc A = 60 độ, tính các góc của hình thang cân BDEC
a) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AB=AC;AD=AE\right)\)
D\(\in\)AB(gt)
E\(\in\)AC(gt)
Do đó: DE//BC(Định lí Ta lét đảo)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 3
Bình luận (0)
Các bạn giúp mình giải mấy bài này với !!!! Mình cảm ơn trước nhé!!Bài 1: Hình thang cân ABCD có AB song song CD, ABCD. Kẻ các đường cao AH, BK. Chứng minh rằng DHCK.Bài 2:Hình thang cân ABCD có AB song song CD, O là giao điểm uaqr 2 đường chéo. Chứng minh rằng OAOB, OCODBài 3: Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bênBài 4: Cho tam giac ABC cân tại A. Lấy điểm D trên cạnh AB, điểm Etrên cạnh AC sao cho ADAEa) Tứ giác...
Đọc tiếp
Các bạn giúp mình giải mấy bài này với !!!! Mình cảm ơn trước nhé!!
Bài 1: Hình thang cân ABCD có AB song song CD, AB<CD. Kẻ các đường cao AH, BK. Chứng minh rằng DH=CK.
Bài 2:Hình thang cân ABCD có AB song song CD, O là giao điểm uaqr 2 đường chéo. Chứng minh rằng OA=OB, OC=OD
Bài 3: Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên
Bài 4: Cho tam giac ABC cân tại A. Lấy điểm D trên cạnh AB, điểm Etrên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì? Vì sao?
b)Các điêm D,E ở vị trí nào thù BD=DE=EC?
Bài 5: Tính các goác của hình thang cân, biết 1 góc bằng 50 độ
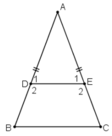
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
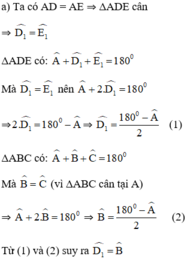
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
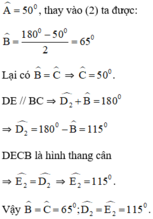
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a. gọi d e f lần lượt là trung điểm của bc ca ab
a) chứng minh tứ giác BDEC là hình thang cân
b) chứng minh tứ giác BDEF là hình bình hành
c) Chứng minh tứ giác là hình thoi
d) Chứng minh tứ AFBR là hình chữ nhật
b: Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔABC
Suy ra: FE//BD và FE=BD
hay BDEF là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD= AE
1.Cm tứ giác BDEC Là hình thang cân
2.tính các góc của hình thang cân
Bài 3:Cho tam giác ABC cân tại A.Gọi D,E,F lần lượt là trung điểm của AB,AC,BC.Gọi điểm I đối xứng với F qua E
a.Chứng minh tứ giác BDEC là hình thang cân
b.Chứng minh tứ giác AFCI là hình chữ nhật
c.Tam giác cân ABC cần có thêm điều kiện gì để hình chữ nhật AFCI là hình vuông?
Bài 4:Cho △ABC vuông tại A,trung tuyến AM.Gọi D là trung điểm của AB,E là điểm đối xứng với M qua D
a.Chứng minh tứ giác AEBM là hình thoi
b.Chứng minh tứ giác AEMC là hình bình hành
c.Tinh diện tích của tam giác A...
Đọc tiếp
Bài 3:Cho tam giác ABC cân tại A.Gọi D,E,F lần lượt là trung điểm của AB,AC,BC.Gọi điểm I đối xứng với F qua E
a.Chứng minh tứ giác BDEC là hình thang cân
b.Chứng minh tứ giác AFCI là hình chữ nhật
c.Tam giác cân ABC cần có thêm điều kiện gì để hình chữ nhật AFCI là hình vuông?
Bài 4:Cho △ABC vuông tại A,trung tuyến AM.Gọi D là trung điểm của AB,E là điểm đối xứng với M qua D
a.Chứng minh tứ giác AEBM là hình thoi
b.Chứng minh tứ giác AEMC là hình bình hành
c.Tinh diện tích của tam giác ABC biết AB=6cm,AC=4cm
Bài 5:Cho △ABC vuông tại A.Gọi D,E,F lần lượt là trung điểm của các cạnh AB,BC,AC.Gọi điểm K đối xứng với E qua AC
a.Các tứ giác ADEF và AKCE là hình gì?Vì sao?
b.Cho AB=4cm và AC=5cm.Tính diện tích tam giác ABC?
Bài 6:Cho △ABC vuông tại A.Gọi M,I,N lần lượt là trung điểm các cạnh AB,BC,AC.Lấy điểm E đối xứng với I qua M
a.Các tứ giác AMIN và AEBI là hình gì?Vì sao?
b.Cho AB=6cm,AC=8cm.Tính diện tích tứ giác AMIN?
HELP ME ![]()
![]()
![]()
bài 9; cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
A, CM; Tứ giác BDEC là thang cân.
B, Cho góc A =70 độ. Tính các góc hình thang cân BDEC.
a, Vì AD = AE nên \(\Rightarrow\Delta ADE\)là tam giác cân tại A
\(\Rightarrow gócADE\)\(=\frac{180^o-A}{2}\)
Vì \(\Delta ABC\)cân tại A nên
Góc CBA = \(\frac{180^o-A}{2}\)
\(\Rightarrow ADE=CBA\)( mà 2 góc này nằm trong vị trí so le trong )
\(\Rightarrow\)\(DE//BC\)
Mà \(ABC=ACB\)(Vì tam giác ABC cân tại A )
\(\Rightarrow\)Tứ giác BDEC là hình thang cân
b,
Ta có :
^A \(=70^o\)\(\Rightarrow\)^B=^C =\(55^O\)
\(\Rightarrow BDE=CED=\frac{\left(360-2\cdot55\right)}{2}=125^O\)
Bài 117. Cho ABC cân ti A. Trên cạnh AB, AC lần lượt lấy các điểm D, E sao cho BD = CE. Chứng minh:
a) ADE cân.
b) DE//BC.
c) T giác BDEC là hình thang cân.
Bài 1: Cho tam giác ABC cân tại A. Hai đường phân giác BE và CD. Chứng minh rằng BDEC là hình thang cân có đáy nhỏ bằng cạnh bên.
Xét ΔABC có
BE là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\left(1\right)\)
Xét ΔABC có
CD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AC}{BC}\left(2\right)\)
Ta có: ΔBAC cân tại A
nên \(AB=AC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
Xét ΔEDC có \(\widehat{EDC}=\widehat{ECD}\left(=\widehat{DCB}\right)\)
nên ΔEDC cân tại E
Suy ra: ED=EC=BD
Đúng 0
Bình luận (0)















