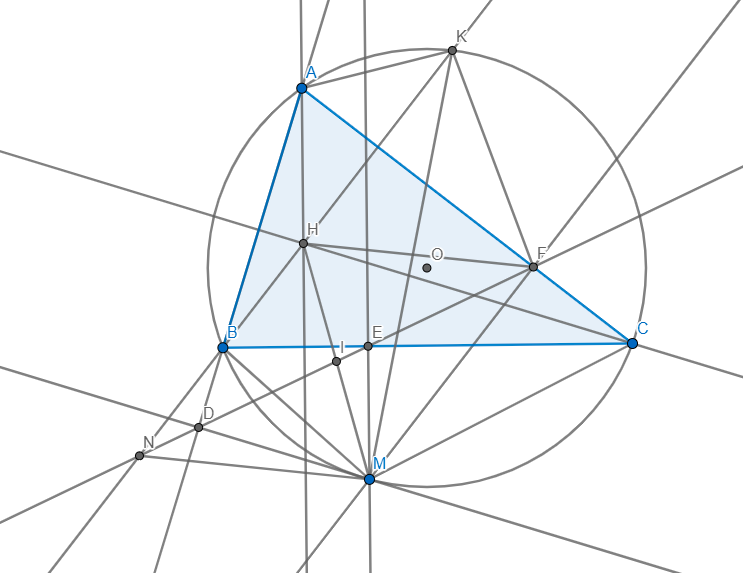
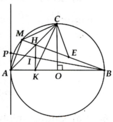
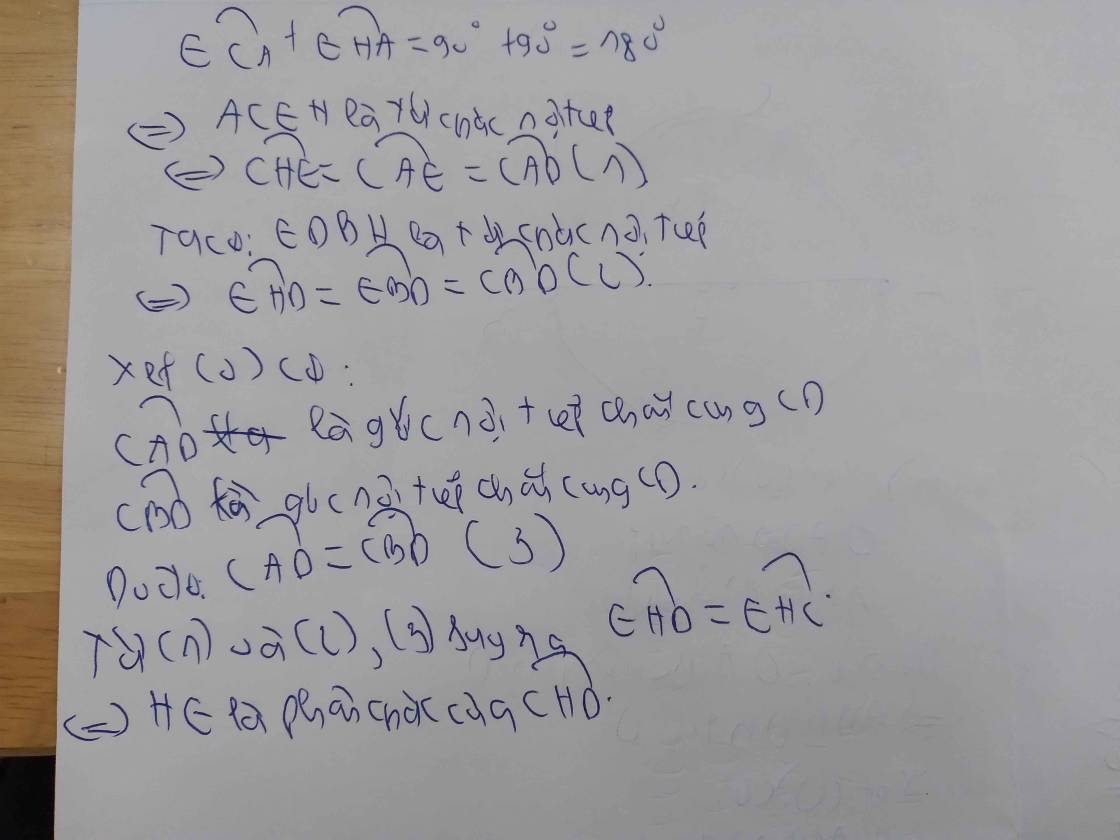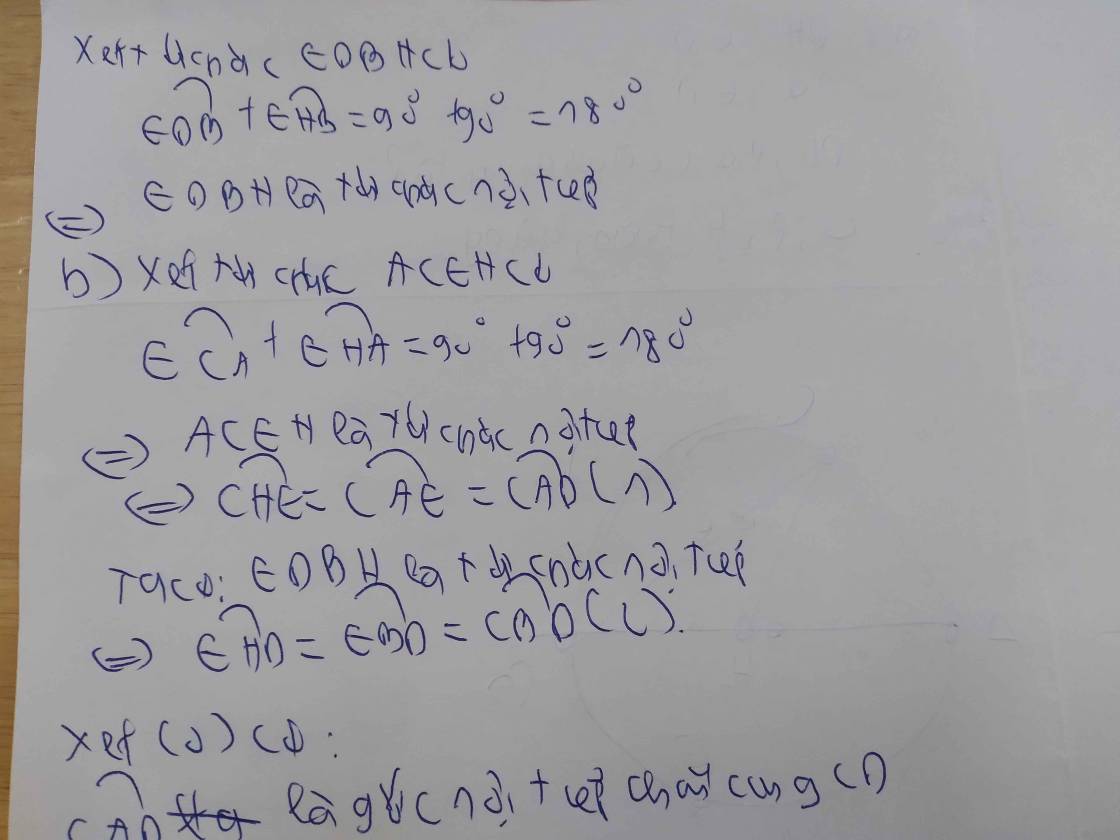Cho DABC nhọn nội tiếp (O). M là một điểm bất kì nằm trên cung nhỏ AC (M khác A và
C, AM < CM). Gọi D, E lần lườt là hình chiếu của M trên AC và BC.
a/ Chứng minh: tứ giác CEDM nội tiếp.
b/ Gọi H là trực tâm của DABC. Gọi gđ của đường thẳng AH với (O) và đường thẳng ED
lần lượt là F và K (F ≠ A). Chứng minh tứ giác MEFK là hình thang cân.
c/ DE cắt MH tại I. Chứng minh I là trung điểm của MH.