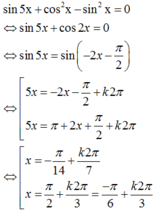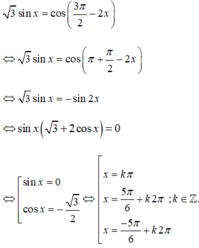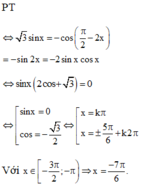Tại sao sinx/2=cos(π/2-x)

Những câu hỏi liên quan
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau:
a, sinx + cosx sqrt{2} sin(x + frac{text{π}}{4}) sqrt{2} cos(x - frac{text{π}}{4})
b, sinx - cosx sqrt{2} sin(x - frac{text{π}}{4}) -sqrt{2} cos(x - frac{text{π}}{4})
c, sin4x - cos4x + sin2x sqrt{2} cos(2x - frac{text{π}}{4})
Đọc tiếp
Chứng minh các đẳng thức sau:
a, sinx + cosx = \(\sqrt{2}\) sin(x + \(\frac{\text{π}}{4}\)) = \(\sqrt{2}\) cos(x - \(\frac{\text{π}}{4}\))
b, sinx - cosx = \(\sqrt{2}\) sin(x - \(\frac{\text{π}}{4}\)) = -\(\sqrt{2}\) cos(x - \(\frac{\text{π}}{4}\))
c, sin4x - cos4x + sin2x = \(\sqrt{2}\) cos(2x - \(\frac{\text{π}}{4}\))
\(sinx+cosx=\sqrt{2}\left(\frac{\sqrt{2}}{2}sinx+\frac{\sqrt{2}}{2}cosx\right)=\sqrt{2}\left(sinx.cos\frac{\pi}{4}+cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)
\(=\sqrt{2}cos\left(\frac{\pi}{2}-\left(x+\frac{\pi}{4}\right)\right)=\sqrt{2}cos\left(\frac{\pi}{4}-x\right)=\sqrt{2}cos\left(x-\frac{\pi}{4}\right)\)
\(sinx-cosx=\sqrt{2}\left(\frac{\sqrt{2}}{2}sinx-\frac{\sqrt{2}}{2}cosx\right)=\sqrt{2}\left(sinx.cos\frac{\pi}{4}-cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\)
\(=-\sqrt{2}sin\left(\frac{\pi}{4}-x\right)=-\sqrt{2}cos\left(\frac{\pi}{2}-\left(\frac{\pi}{4}-x\right)\right)=-\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(sin^4x-cos^4x=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)+sin2x\)
\(=sin^2x-cos^2x+sin2x=sin2x-cos2x\)
\(=\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)\)
Bạn ghi ko đúng đề
Đúng 0
Bình luận (0)
Tìm x biết ba số cos(x-π/4); sinx; cos(x+π/4) là 3 số hạng liên tiếp của cấp số nhân
Để \(cos\left(x-\dfrac{\Omega}{4}\right);sinx;cos\left(x+\dfrac{\Omega}{4}\right)\) là ba số hạng liên tiếp của cấp số nhân thì \(sin^2x=cos\left(x-\dfrac{\Omega}{4}\right)\cdot cos\left(x+\dfrac{\Omega}{4}\right)\)
=>\(sin^2x=\sqrt{2}\left(cosx-sinx\right)\cdot\sqrt{2}\left(cosx+sinx\right)\)
=>\(sin^2x=2cos^2x-2sin^2x\)
=>\(3\cdot sin^2x=2\cdot cos^2x\)
=>\(\dfrac{sin^2x}{cos^2x}=\dfrac{2}{3}\)
=>\(tan^2x=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}tanx=\dfrac{\sqrt{6}}{3}\\tanx=-\dfrac{\sqrt{6}}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=arctan\left(\dfrac{\sqrt{6}}{3}\right)+k\Omega\\x=arctan\left(-\dfrac{\sqrt{6}}{3}\right)+k\Omega\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Trong các đẳng thức sau, đẳng thức nào đúng, đẳng thức nào sai?
cos(x + π/2) = sinx
4sin3x+3sin2xcosx-sinx-cos3x=0cos3x+sin3x=sinx-cosx(tanx+1)sin2x=3(cosx-sinx)sinx+3sin3(x-\({ π \over 4}\))=\(\sqrt2 sinx\)
Xem chi tiết
câu 1:xét sinx=o
xét sinx khác 0
chia phương trình cho cos3x
ta được 1 phương trình mới:
4+3tanx-\(\frac{1}{sin^2x}\)-tan3x=0
<=>4+3tanx-(1+cot2x)-tan3x=0
<=>4+3tanx-1-\(\frac{1}{tan^2x}\)-tan3x=o
nhân cho tan2x ta được 1 phương trình bậc 5 với tanx
Đúng 0
Bình luận (0)
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
f
(
x
)
1
+
cos
x
(
x
-...
Đọc tiếp
f ( x ) = 1 + cos x ( x - π ) 2 , k h i x ≠ π m , k h i x = π Tìm m để f (x) liên tục tại x = π
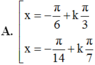
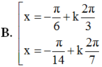
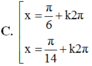

Tìm nghiệm thuộc
-
π
3
;
-
π
của phương trình
3
sinx cos
3
π
2
-
2
x
A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Tìm nghiệm thuộc - π 3 ; - π của phương trình
3 sinx = cos 3 π 2 - 2 x
A. 0
B. 1
C. 2
D. 3
Tìm số nghiệm thuộc
[
-
3
π
2
;
-
π
)
của phương trình
3
sinx cos
3
π
2
-
2
x
A. 0. B. 1. C. 2. D. 3
Đọc tiếp
Tìm số nghiệm thuộc [ - 3 π 2 ; - π ) của phương trình
3 sinx = cos 3 π 2 - 2 x
A. 0.
B. 1.
C. 2.
D. 3