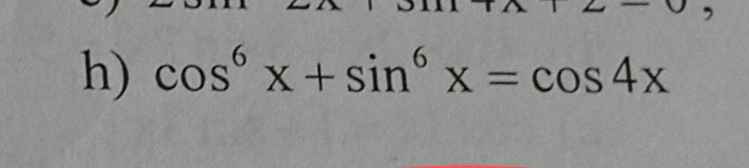 giai chi tiết giúp e với!!!
giai chi tiết giúp e với!!!

Những câu hỏi liên quan
Giai bằng cách lập phương trình giúp mik với . Giải chi tiết hộ mik ạ . Mik cảm ơn nhiền
gọi x là vận tốc của ô tô
y là vận tốc của xe máy (km/h) (x>y>0)
sau 4h 2 xe gặp nhau nên tổng quãng đường AB bằng:
AB= 4.x+4.y = 4.(x+y) (km)
nên thgian ô tô và xe máy đi hết AB lần lượt là:
Đúng 0
Bình luận (0)
Gọi thời gian xe máy đi hết quãng đường AB là x (h) (x>4)
thời gian xe máy đi hết quãng đường AB là y (h) (y>4)
Trong 1 giờ xe máy đi được \(\dfrac{1}{x}\) (quãng đường)
Trong 1 giờ ô tô đi được \(\dfrac{1}{y}\) (quãng đường)
Trong 1 giờ hai xe đi được \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Mà thời gian ô tô về đến A sớm hơn xe máy về đến B là 6 giờ nên: \(x-y=6\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\x-y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{x-6}=\dfrac{1}{4}\\y=x-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-14x+24=0\\y=2-6\end{matrix}\right.\)(ĐK:\(x\ne6\)) \(\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\)(TM)
Vậy thời gian xe máy đi hết quãng đường AB là 12 giờ
thời gian ô tô đi hết quãng đường AB là 6giờ
-Chúc bạn học tốt-
Đúng 0
Bình luận (0)
Giai chi tiết giúp mik vs
trình tự các ribonucleotit trong phân tử ARN được tổng hợp từ gen trên là:
5'AUG XAU GXA UAX GTU TAA 3'
Đúng 1
Bình luận (0)
Giúp chi tiết giúp e với ạ🥺
1.
$(m^2-m-1)x-5m=(3-m)x$
$\Leftrightarrow (m^2-m-1+m-3)x=5m$
$\Leftrightarrow (m^2-4)x=5m$
$\Leftrightarrow (m-2)(m+2)x=5m$
Nếu $m=-2$ thì $0x=-10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m=2$ thì $0x=10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m\neq \pm 2$ thì pt có nghiệm duy nhất $x=\frac{5m}{(m-2)(m+2)}$
Đúng 1
Bình luận (0)
2.
$m^2x+mx+x-m-2=0$
$\Leftrightarrow x(m^2+m+1)=m+2$
Vì $m^2+m+1=(m+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow m^2+m+1\neq 0$
Do đó pt có nghiệm duy nhất $x=\frac{m+2}{m^2+m+1}$ với mọi $m\in\mathbb{R}$
Đúng 1
Bình luận (0)
Giúp e giải chi tiết với ạ, e cảm ơn
Giải chi tiết giúp e với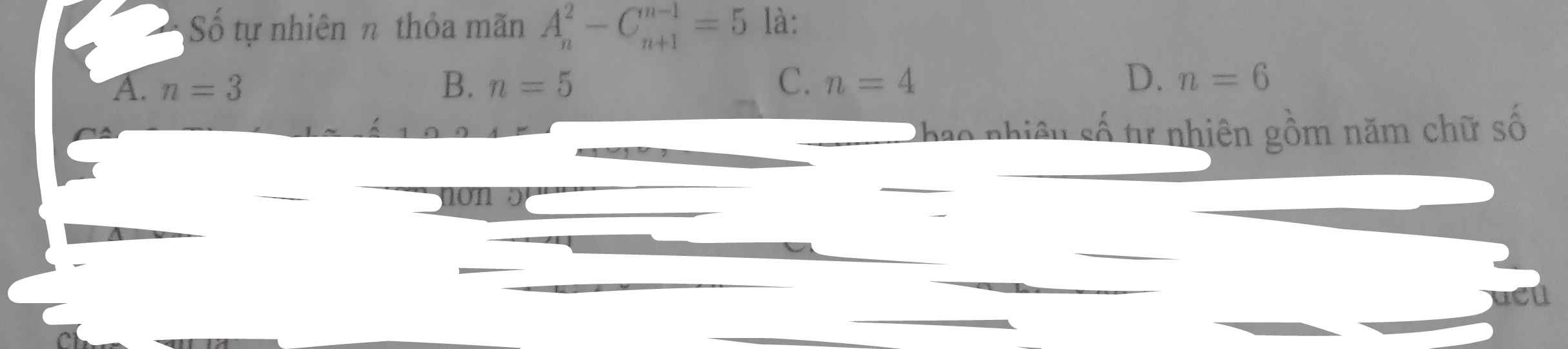
Lời giải:
Đẳng thức \(\Leftrightarrow \frac{n!}{(n-2)!}-\frac{(n+1)!}{(n-1)!2!}=5\)
\(\Leftrightarrow n(n-1)-\frac{n(n+1)}{2}=5\)
\(\Leftrightarrow n^2-3n-10=0\Leftrightarrow (n-5)(n+2)=0\)
Vì $n$ tự nhiên nên $n=5$. Đáp án B.
Đúng 0
Bình luận (0)
Giải chi tiết giúp e với
Có \(2!=2\) cách xếp 2 người nhóm 1 kề nhau
Có \(3!=6\) cách xếp 3 người nhóm 2 kề nhau
Coi 2 người nhóm 1 là 1 bó và 3 người nhóm 2 là 1 bó (chiếm 5 vị trí nên còn 2 vị trí trống trong 7 vị trí)
Chọn 2 vị trí trong 4 vị trí: \(A_4^2=12\) cách
Theo quy tắc nhân có: \(2.6.12=144\) cách
Đúng 2
Bình luận (0)
Giải chi tiết giúp e với
Bạn lưu ý chuyển bài toán vào đúng mục xác suất trong toán 11, không phải hàm số lượng giác.
Đúng 0
Bình luận (0)
Lời giải:
Gọi số có 3 chữ số phân biệt được lập từ $0,1,2,3$ là $\overline{a_1a_2a_3}$.
$A$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1$ có thể bằng $0,1,2,3$
$B$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1\neq 0$ (chính là số thỏa đề)
$C$ là tập các số $\overline{a_1a_2a_3}$ mà $a_1=0$
Tại tập $A$ thì mỗi số $0,1,2,3$ xuất hiện $18$ lần ở 3 vị trí hàng chục, trăm, đơn vị.
Tổng chữ số tập $A$:
$\frac{1}{3}.18(0+1+2+3)(10^2+10+1)=3996$
Tổng chữ số tập $C$ là:
$012+021+013+031+023+032=132$
Tồng các chữ số tập $B$ là:
$3996-132=3864$
Tổng các chữ số tập $B$:
$11988-132=11856$
Đúng 0
Bình luận (0)
Một hướng khác là bạn có thể viết ra $18$ số thỏa mãn đề và cộng lại với nhau.
Đúng 0
Bình luận (0)
Với mọi số tự nhiên n chứng tỏ số C=tối giai
Giải chi tiết giúp mình nhé
Giúp e giải chi tiết với ạ e cảm ơn ạ


















