Cho hình bình hành ABCD, các cạnh AB, CD lần lượt lấy các điểm M, N sao cho AM=DN. đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E, F. c/m rằng E và F đối xứng qua MB

Những câu hỏi liên quan
Cho hình bình hành ABCD, các cạnh AB, CD lần lượt lấy các điểm M, N sao cho AM=DN. đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E, F. c/m rằng E và F đối xứng qua MB
Cho mình xin hình vẽ nữa !
Cho hình bình hành ABCD, trên các cạnh AB,CD lần lượt lấy các điểm M,N sao cho AM=DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN tại E,F. Chứng minh rằng:
a, E và F đối xứng qua AB
b, MEBF là hình thoi
c, Hình bình hành ABCD phải có điều kiện gì để BCNE là hình thang cân?
Cho hình bình hành ABCD trên cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM=DN Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F Chứng minh rằng
a) E và F đối xứng qua AB
b) Tứ giác MEBF là hình thoi
c) Hình bình hành ABCD phải có điều kiện gì để tứ giác BCNE là hình thang cân
BÀI 1: Gọi I là giao điểm của EF và AB
Vì EF là đường trung trực của MB nên BE = BF
Xét hai tam giác BEI và BFI thì chúng bằng nhau ( t.hợp ch-cgv)
=> IE = IF; EF vuông góc AB
=> E và F đối xứng nhau qua AB
* xét tứ giác MEBF có :
- EM = EB; FM = FB ( È là đường trung trực của MB)
mà E và F đối xứng nhau qua AB nên ta c/m được hai tam giác BEI và BFI bằng nhau ( t.hợp ch-cgv)
=> EM = EB = FM = FB
=> MEBF là hình thoi
*Vì EB // NC nên EBCN là hình thang có 2 đáy là EB và NC
để EBCN là hình thang cân thì EN = BC
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD trên cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM=DN Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F Chứng minh rằng
a) E và F đối xứng qua B
b) Tứ giác MEBF là hình thoi
c) Hình bình hành ABCD phải có điều kiện gì để tứ giác BCNE là hình thang cân
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F. a) Chứng minh tứ giác AMND là hình bình hành. b) Chứng minh rằng tứ giác MEBF là hình thoi. c) Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm MvàN sao cho AM DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.a) Chứng minh E và F đối xứng với nhau qua AB.b) Chứng minh tứ giác MEBF là hình thoi c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
Đọc tiếp
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm MvàN sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.
a) Chứng minh E và F đối xứng với nhau qua AB.
b) Chứng minh tứ giác MEBF là hình thoi
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
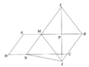
a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD, trên các cạnh AB và CD lần lượt lấy các điểm M,N sao cho AM=DN. Đường trung trực của Bm lần lượt cắt các đường thẳng MN và BC tại E và F.CMR:
a) E và F đối xứng với nhau qua D
b) Tứ giác MEBF là hình thoi
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM=DN. Đường trung trực của BM lần lượt cắt các đương thẳng MN và BC tại E và F. Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân?
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm MvàN sao cho AM DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.a) AB là đường trung trực của đoạn thẳng EF
Đọc tiếp
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm MvàN sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.
a) AB là đường trung trực của đoạn thẳng EF
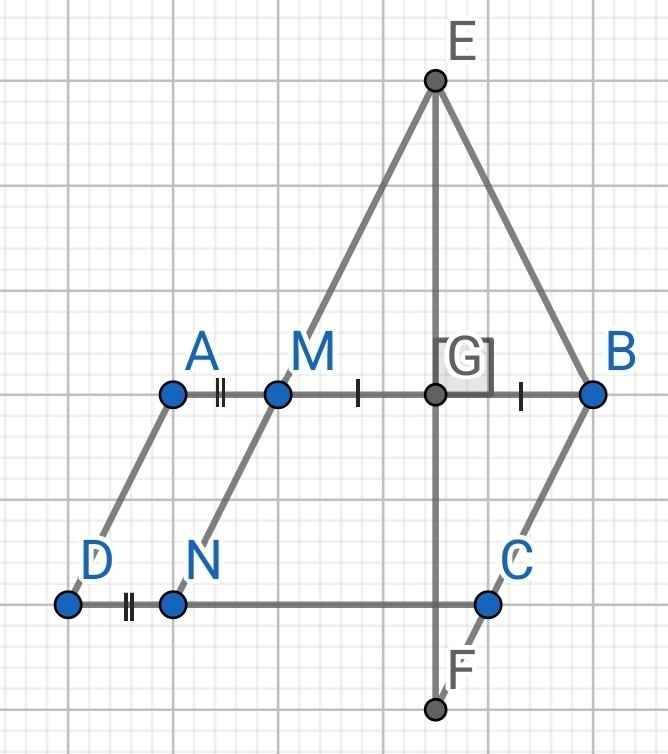 Do ABCD là hình bình hành
Do ABCD là hình bình hành
⇒ AB // CD
⇒ AM // DN
Tứ giác AMND có:
AM = DN (gt)
AM // DN (cmt)
⇒ AMND là hình bình hành
⇒ MN // AD
Mà AD // BC (ABCD là hình bình hành)
⇒ MN // BC
⇒ ∠GME = ∠GBF (so le trong)
Do EF là đường trung trực của BM
⇒ GM = GB
Xét hai tam giác vuông: ∆GME và ∆GBF có:
GM = GB (cmt)
∠GME = ∠GBF (cmt)
⇒ ∆GME = ∆GBF (cạnh góc vuông-góc nhọn kề)
⇒ GE = GF (hai cạnh tương ứng)
⇒ G là trung điểm của EF
Mà BM ⊥ EF
⇒ BM là đường trung trực của EF
Hay AB là đường trung trực của EF
Đúng 2
Bình luận (0)
















