mn vẽ lại hình giúp mình ạ

Những câu hỏi liên quan
Giúp mình b13 với ạ! (0 cần vẽ hình đâu nhé)
Camon mn trc ạ, mình cần gấp :((
mn giúp mình câu b nhé, vẽ thêm cả hình giúp mình nx ạ, mình thấy ý này khoai khoai

a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
Đúng 2
Bình luận (0)
mn ơi giúp mình vẽ 3 cái hình chiếu của cái hình này với ạ :((((
Xin lũi vẽ bằng máy nên hơi xấu với độ Cm ko chuẩn ( muốn căn cho bằng nhau r mà ko đc)
Đúng 0
Bình luận (0)

Ai giúp mình phần 2 nhỏ bài tìm gtri nguyên n với câu 3 bài hình đc ko ạ(kèm vẽ hình) nếu cần thiết mn làm giúp e câu 5 ạ ko thì thôi ạ. Mình cảm ơn nhiều
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Đúng 2
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ AB. Vẽ AH vuông góc với CD. CMR: CH=\(\dfrac{CD+AB}{2}\). mn giúp mình vs ạ, mình đang cần gấp ạ. <33 Thanks mn nhiều.
giải chi tiết ra giúp mình luôn ạ, vẽ hình luôn, hôm nay mik phải nọp rùi, mình cảm ơn mn rât nhiều

1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)
Đúng 2
Bình luận (0)
giúp mình vẽ lại hình đó và làm bài đó ạ.
a, \(=>R5nt\left[\left(R1ntR3\right)//\left(R2ntR4\right)\right]\)
\(=>Rtd=R5+\dfrac{\left(R1+R3\right)\left(R2+R4\right)}{R1+R2+R3+R\text{4}}\)
\(=2+\dfrac{\left(3+1\right)\left(2+2\right)}{3+1+2+2}=4\left(om\right)\)
b,\(=>Im=\dfrac{20}{4}=5A=I5\)\(=I1234\)
\(=>U1234=5.\dfrac{\left(3+1\right)\left(2+2\right)}{3+1+2+2}=10V=U24\)
\(=>I24=\dfrac{10}{2+2}=2,5A=IA\)
Đúng 1
Bình luận (2)
Cho hình vẽ sau: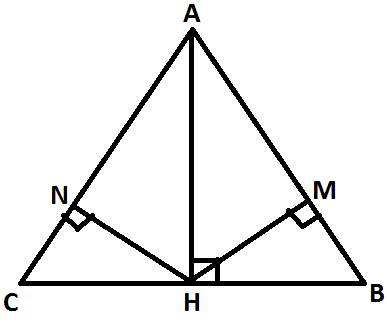
Cho Å1 =Å2
MN⊥AC
HM⊥AB
a, CM ΔAHC=ΔAHB
b, CM ΔHNC=ΔHMB
mọi người giải giúp mình với, mình c.ơn trước ạ:33
Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)
Đúng 2
Bình luận (3)
Mong mn giúp ạ,vẽ hình nx ạ. :3
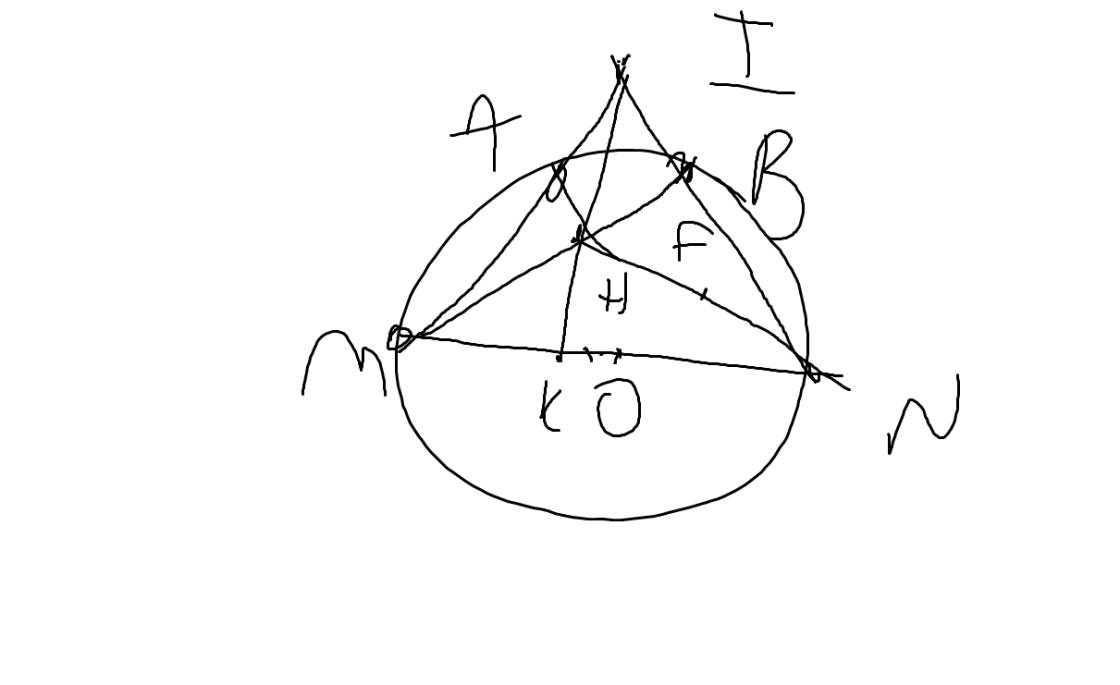
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN
Đúng 3
Bình luận (0)





















