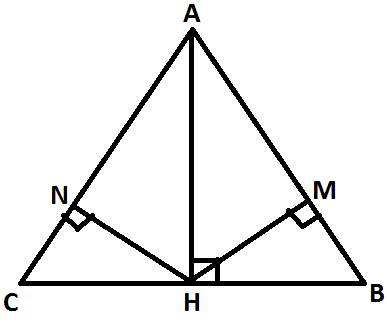
Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)