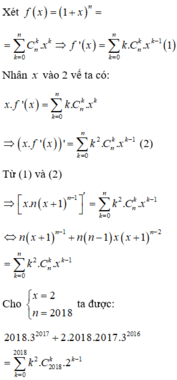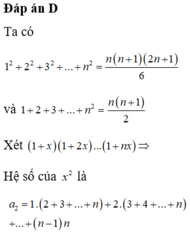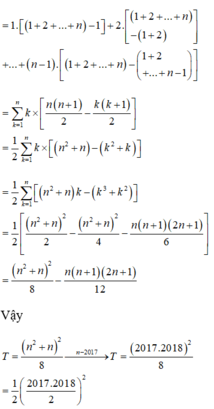1. 

$=153^2+2.47.153+47^2=(153+47)^2=200^2=40000$

2.

$=1,24^2-2.1,24.0,24+0,24^2=(1,24-0,24)^2=1^2=1$

3. Không phù hợp để tính nhanh 

4. 

$=15^8-(15^8-1)=1$

5.

$=(1^2-2^2)+(3^2-4^2)+(5^2-6^2)+...+(2019^2-2020^2)$

$=(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+...+(2019-2020)(2019+2020)$

$=(-1)(1+2)+(-1)(3+4)+(-1)(5+6)+....+(-1)(2019+2020)$

$=(-1)(1+2+3+4+....+2019+2020)=(-1).2020(2020+1):2=-2041210$

6:

\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =1.\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^4-1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^8-1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^{2020}-1\right)\left(2^{2020}+1\right)+1\\ =2^{4040}-1+1=2^{4040}\)

a. Ta có: \(17^2-14.17+49=17^2-2.7.17+7^2=\left(17-7\right)^2=10^2=100\)

b. \(2021^2-2020^2=\left(2021-2020\right)\left(2021+2020\right)=4041\)

Đáp án C

\(a,12.\dfrac{-7}{11}.\dfrac{5}{6}.\dfrac{22}{7}=\left(12.\dfrac{5}{6}\right)\left(\dfrac{-7}{11}.\dfrac{22}{7}\right)=10.\left(-2\right)=-20\\ b,\dfrac{-8}{15}.\dfrac{7}{9}.\dfrac{5}{8}.\left(-18\right)=\left(\dfrac{-8}{15}.\dfrac{5}{8}\right)\left[\dfrac{7}{9}.\left(-18\right)\right]=\dfrac{-1}{3}.\left(-14\right)=\dfrac{14}{3}\)

a) 12.−711.56.227= (12.56)(−711.227)= 10.(−2)= −20.

b) −815.79.58.(−18)= (−815.58)[79.(−18)]= −13.(−14)= 143.

Đáp án D

Ta có 1 2 + 2 2 + 3 2 + ... + n 2 = n n + 1 2 n + 1 6

và 1 + 2 + 3 + ... + n 2 = n n + 1 2

Xét 1 + x 1 + 2 x ... 1 + n x ⇒ Hệ số của x 2 là

  a 2 = 1. 2 + 3 + ... + n + 2. 3 + 4 + ... + n + ... + n − 1 n

= 1. 1 + 2 + ... + n − 1 + 2. 1 + 2 + ... + n − 1 + 2 + ... + n − 1 . 1 + 2 + ... + n − 1 + 2 + ... + n − 1

= ∑ k = 1 n k × n n + 1 2 − k k + 1 2

= 1 2 ∑ k = 1 n k × n 2 + n − k 2 + k

= 1 2 ∑ k = 1 n n 2 + n k − k 3 + k 2

= 1 2 = n 2 + n 2 8 − n n + 1 2 n + 1 12

n 2 + n 2 2 − n 2 + n 2 4 − n n + 1 2 n + 1 6

Vậy  T = n 2 + n 2 8

→ n − 2017 T = 2017.2018 2 8 = 1 2 2017.2018 2 2

a) \(\left(-48\right)+10+\left(-22\right)+\left(-10\right)\)

\(=\left[\left(-48\right)+\left(-22\right)\right]+\left(-10+10\right)\)

\(=-70+0=-70\)

Tham khảo <3

= -70 

( hihi )

(-48)+(-22)+(10-10)

=-70 +0

=-70

`b)48/100+22/100+5/100+25/100`

`=>(48/100+22/100)+(5/100+25/100)`

`=>70/100+70/100`

`=>100/100=1`

a,3,31x5+6x3,31-3,31                       

=3,31x(5+6-1)

=3,31x10

=33,1

b) 48/100+22%+5/100+0,25

=48%+22%+5%+25%

=1

a,3,31x5+6x3,31-3,31       

=3,31x5+6x3,31-3,31x1

=3,31 x ( 5+6-1)

= 3,31 x10

= 33,1

 b,48/100+22%+5/100+0,25

= 0,48 +0,22 + 0,05 +0,25

=    1