Đại số hoá pt lượng giác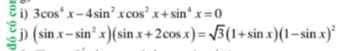

Những câu hỏi liên quan
Đại số hoá pt lượng giác
b)Thấy sinx=0 không là nghiệm của pt
Chia cả hai vế của pt cho \(sin^3x\) ta được:
\(\dfrac{1}{sin^2x}-4+\dfrac{cosx}{sinx}.\dfrac{1}{sin^2x}=0\)
\(\Leftrightarrow1+cot^2x-4+cotx\left(1+cot^2x\right)=0\)
\(\Leftrightarrow cot^3x+cot^2x+cotx-3=0\)
\(\Leftrightarrow cotx=1\)\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\left(k\in Z\right)\)
Vậy...
k) Pt \(\Leftrightarrow\left(sinx-cosx\right)\left(sin^2x+sinx.cosx+cos^2x\right)=sinx+cosx\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(1+sinx.cosx\right)=sinx+cosx\)
\(\Leftrightarrow sin^2x.cosx-sinx.cos^2x-2cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin^2x-sinx.cosx-2=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\-sin^2x-sinx.cosx-2cos^2x=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{\pi}{2}+k\pi\) (\(k\in Z\))
Vậy...
Đúng 0
Bình luận (0)
Đại số hoá pt lượng giác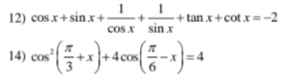
12.
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(cosx+sinx+\dfrac{1}{cosx}+\dfrac{1}{sinx}+tanx+cotx=-2\)
\(\Leftrightarrow cosx+sinx+\dfrac{cosx+sinx}{cosx.sinx}+\dfrac{sin^2x+cos^2x+2sinx.cosx}{sinx.cosx}=0\)
\(\Leftrightarrow cosx+sinx+\dfrac{cosx+sinx}{cosx.sinx}+\dfrac{\left(sinx+cosx\right)^2}{sinx.cosx}=0\)
\(\Leftrightarrow\left(cosx+sinx\right)\left(1+\dfrac{1}{cosx.sinx}+\dfrac{sinx+cosx}{sinx.cosx}\right)=0\)
\(\Leftrightarrow\dfrac{\left(cosx+sinx\right)\left(sinx+1\right)\left(cosx+1\right)}{sinx.cosx}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx+sinx=0\\sinx+1=0\\cosx+1=0\end{matrix}\right.\)
TH1: \(cosx+sinx=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\left(tm\right)\)
TH2: \(sinx+1=0\)
\(\Leftrightarrow sinx=-1\)
\(\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\left(l\right)\)
TH3: \(cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\left(l\right)\)
Vậy phương trình đã cho có nghiệm \(x=-\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
14.
\(cos^2\left(\dfrac{\pi}{3}+x\right)+4cos\left(\dfrac{\pi}{6}-x\right)=4\)
\(\Leftrightarrow sin^2\left(\dfrac{\pi}{6}-x\right)+4cos\left(\dfrac{\pi}{6}-x\right)-4=0\)
\(\Leftrightarrow cos^2\left(\dfrac{\pi}{6}-x\right)+4cos\left(\dfrac{\pi}{6}-x\right)-5=0\)
\(\Leftrightarrow\left[cos\left(\dfrac{\pi}{6}-x\right)-1\right].\left[cos\left(\dfrac{\pi}{6}-x\right)+5\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{6}-x\right)=1\\cos\left(\dfrac{\pi}{6}-x\right)=-5\left(l\right)\end{matrix}\right.\)
\(cos\left(\dfrac{\pi}{6}-x\right)=1\Leftrightarrow\dfrac{\pi}{6}-x=0\Leftrightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{6}\)
Đúng 0
Bình luận (0)
Đại số hoá pt lượng giác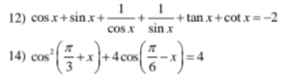
14)\(cos^2\left(\dfrac{\pi}{3}+x\right)+4cos\left(\dfrac{\pi}{6}-x\right)=4\)
\(\Leftrightarrow-sin^2\left(\dfrac{\pi}{3}+x\right)+1+4.sin\left(\dfrac{\pi}{3}+x\right)=4\)
\(\Leftrightarrow-sin^2\left(\dfrac{\pi}{3}+x\right)+4sin\left(\dfrac{\pi}{3}+x\right)-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(\dfrac{\pi}{3}+x\right)=3\left(vn\right)\\sin\left(\dfrac{\pi}{3}+x\right)=1\end{matrix}\right.\)\(\Rightarrow x=\dfrac{\pi}{6}+k2\pi,k\in Z\)
Vậy...
Đúng 2
Bình luận (0)
12) ĐKXĐ: cosx , sinx≠0
pt <=> (cosx + 1) + ( sinx + 1) +\(\dfrac{1+cosx}{sinx}\)+ \(\dfrac{1+sinx}{cosx}\)
=0
<=> (cosx + 1 ) ( 1+ \(\dfrac{1}{sinx}\) ) + ( sinx+1)(1 + \(\dfrac{1}{cosx}\) ) = 0
<=> ( cosx + 1) ( sinx + 1) ( \(\dfrac{1}{sinx}\) + \(\dfrac{1}{cosx}\) ) = 0
<=> cos x = -1
hoặc sinx = -1
hoặc sinx + cos x = 0
Đúng 1
Bình luận (0)
Đại số hoá pt lượng giác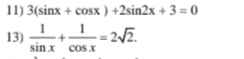
11.
Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow sin2x=2sinx.cosx=t^2-1\)
Phương trình đã cho tương đương:
\(3t+2t^2+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{2}\end{matrix}\right.\)
TH1: \(t=-1\)
\(\Leftrightarrow sinx+cosx=-1\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=cos\dfrac{3\pi}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
TH2: \(t=-\dfrac{1}{2}\)
\(\Leftrightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x-\dfrac{\pi}{4}=-arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}\pm arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\)
Vậy ...
Đúng 1
Bình luận (0)
13.
ĐK: \(x\ne\dfrac{\pi}{2}+\dfrac{k\pi}{2}\)
Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình đã cho tương đương:
\(\dfrac{sinx+cosx}{sinx.cosx}=2\sqrt{2}\)
\(\Leftrightarrow\dfrac{2t}{t^2-1}=2\sqrt{2}\)
\(\Leftrightarrow t=\sqrt{2}t^2-\sqrt{2}\)
\(\Leftrightarrow t=\sqrt{2}t^2-\sqrt{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{\sqrt{2}}{2}\\t=-\sqrt{2}\end{matrix}\right.\)
TH1: \(t=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sinx+cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\left(l\right)\\x=k2\pi\left(l\right)\end{matrix}\right.\)
TH2: \(t=-\sqrt{2}\)
\(\Leftrightarrow sinx+cosx=-\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-\sqrt{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\pi+k\pi\\x-\dfrac{\pi}{4}=-\pi+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{4}+k\pi\left(tm\right)\\x=-\dfrac{3\pi}{4}+k\pi\left(tm\right)\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Đại số hoá pt lượng giác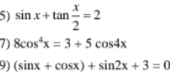
a.
\(sinx=2sin\dfrac{x}{2}cos\dfrac{x}{2}=\dfrac{2sin\dfrac{x}{2}.cos\dfrac{x}{2}}{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}}=\dfrac{2tan\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}\)
Pt tương đương: \(\dfrac{2tan\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}+tan\dfrac{x}{2}=2\)
Đặt \(tan\dfrac{x}{2}=t\) ta được:
\(\dfrac{2t}{1+t^2}+t=2\Leftrightarrow2t+t\left(1+t^2\right)=2+2t^2\)
\(\Leftrightarrow t^3-2t^2+3t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2-t+2\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow tan\dfrac{x}{2}=1\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (2)
7.
\(\Leftrightarrow2\left(2cos^2x\right)^2=3+5\left(2cos^22x-1\right)\)
\(\Leftrightarrow2\left(cos2x+1\right)^2=10cos^22x-2\)
\(\Leftrightarrow2cos^22x-cos2x-1=0\)
Đặt \(cos2x=t\Rightarrow2t^2-t-1=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k2\pi\\2x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
9.
Đặt \(sinx+cosx=t\) với \(\left|t\right|\le\sqrt{2}\)
\(\Rightarrow t^2=sin^2x+cos^2x+2sinx.cosx=1+sin2x\)
\(\Rightarrow sin2x=t^2-1\)
Phương trình trở thành:
\(t+t^2-1+3=0\)
\(\Leftrightarrow t^2+t+2=0\) (vô nghiệm)
Đúng 0
Bình luận (0)
Đại số hoá pt lượng giác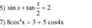
5.
ĐK: \(x\ne\pi+k2\pi\)
Đặt \(t=tan\dfrac{x}{2}\Rightarrow sinx=\dfrac{2t}{1+t^2}\)
Phương trình trở thành:
\(\dfrac{2t}{1+t^2}+t=2\)
\(\Leftrightarrow2t+t+t^3=2+2t^2\)
\(\Leftrightarrow t^3-2t^2+3t-2=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow tan\dfrac{x}{2}=1\)
\(\Leftrightarrow sin\dfrac{x}{2}=cos\dfrac{x}{2}\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 2
Bình luận (0)
7.
\(\Leftrightarrow8\left(\dfrac{1+cos2x}{2}\right)^2=3+5\left(2cos^22x-1\right)\)
Đặt \(cos2x=t\) ta được:
\(8\left(\dfrac{t+1}{2}\right)^2=3+5\left(2t^2-1\right)\)
\(\Leftrightarrow2t^2-t-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{3}+k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cácbon là nguyên tố hoá học đăc biệt quan trọng trong việc tạo nên sự đa dạng của các đại phân tử hữu cơ vì cacbon
C. có cấu hình điện tử vòng ngoài với 4 điện tử (cùng lúc tạo nên 4 liên kết cộng hoá trị với nguyên tử khác).
Đúng 0
Bình luận (0)
Khi thực hiện phản ứng este hoá 1 mol CH3COOH và 1 mol C2H5OH, lượng este lớn nhất thu được là 2/3 mol. Để đạt hiệu suất cực đại là 80% (tính theo axit) khi tiến hành este hoá 1 mol CH3COOH cần số mol C2H5OH là (biết các phản ứng este hoá thực hiện ở cùng nhiệt độ) A. 0,4 B. 0,8 C. 1,6 D. 3,2
Đọc tiếp
Khi thực hiện phản ứng este hoá 1 mol CH3COOH và 1 mol C2H5OH, lượng este lớn nhất thu được là 2/3 mol. Để đạt hiệu suất cực đại là 80% (tính theo axit) khi tiến hành este hoá 1 mol CH3COOH cần số mol C2H5OH là (biết các phản ứng este hoá thực hiện ở cùng nhiệt độ)
A. 0,4
B. 0,8
C. 1,6
D. 3,2
Đáp án C
Phương trình hóa học:
CH3COOH + C2H5OH D CH3COOC2H5 + H2O
Ban đầu: 1 1
Phản ứng: 2/3 2/3 2/3 2/3
Cân bằng: 1/3 1/3 2/3 2/3
Hằng số cân bằng:

Vì H = 80% (tính theo axit) nên naxit(pu) = 0,8 mol
CH3COOH + C2H5OH D CH3COOC2H5 +H2O
Ban đầu: 1 x
Phản ứng:0,8à 0,8 à 0,8 à 0,8
Cân bằng:0,2 (x-0,8) 0,8 0,8
Hằng số cân bằng:
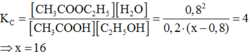
Đúng 0
Bình luận (0)
Khi thực hiện phản ứng este hoá 1 mol CH3COOH và 1 mol C2H5OH, lượng este lớn nhất thu được là 2/3 mol. Để đạt hiệu suất cực đại là 80% (tính theo axit) khi tiến hành este hoá 1 mol CH3COOH cần số mol C2H5OH là (biết các phản ứng este hoá thực hiện ở cùng nhiệt độ) A. 0,4 B. 0,8 C. 1,6 D. 3,2
Đọc tiếp
Khi thực hiện phản ứng este hoá 1 mol CH3COOH và 1 mol C2H5OH, lượng este lớn nhất thu được là 2/3 mol. Để đạt hiệu suất cực đại là 80% (tính theo axit) khi tiến hành este hoá 1 mol CH3COOH cần số mol C2H5OH là (biết các phản ứng este hoá thực hiện ở cùng nhiệt độ)
A. 0,4
B. 0,8
C. 1,6
D. 3,2
Đáp án C
Phương trình hóa học:
CH3COOH + C2H5OH D CH3COOC2H5 + H2O
Ban đầu: 1 1
Phản ứng: 2/3 2/3 2/3 2/3
Cân bằng: 1/3 1/3 2/3 2/3
Hằng số cân bằng:
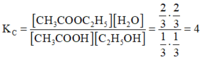
Vì H = 80% (tính theo axit) nên naxit(pu) = 0,8 mol
CH3COOH + C2H5OH D CH3COOC2H5 +H2O
Ban đầu: 1 x
Phản ứng:0,8à 0,8 à 0,8 à 0,8
Cân bằng:0,2 (x-0,8) 0,8 0,8
Hằng số cân bằng:
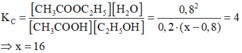
Đúng 0
Bình luận (0)











