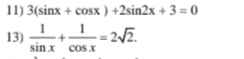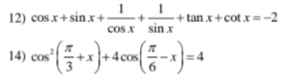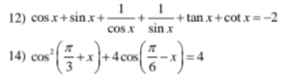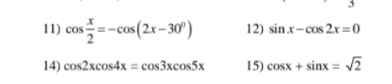11.
Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow sin2x=2sinx.cosx=t^2-1\)
Phương trình đã cho tương đương:
\(3t+2t^2+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{2}\end{matrix}\right.\)
TH1: \(t=-1\)
\(\Leftrightarrow sinx+cosx=-1\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=cos\dfrac{3\pi}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
TH2: \(t=-\dfrac{1}{2}\)
\(\Leftrightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x-\dfrac{\pi}{4}=-arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}\pm arccos\left(-\dfrac{1}{2\sqrt{2}}\right)+k2\pi\)
Vậy ...
13.
ĐK: \(x\ne\dfrac{\pi}{2}+\dfrac{k\pi}{2}\)
Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình đã cho tương đương:
\(\dfrac{sinx+cosx}{sinx.cosx}=2\sqrt{2}\)
\(\Leftrightarrow\dfrac{2t}{t^2-1}=2\sqrt{2}\)
\(\Leftrightarrow t=\sqrt{2}t^2-\sqrt{2}\)
\(\Leftrightarrow t=\sqrt{2}t^2-\sqrt{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{\sqrt{2}}{2}\\t=-\sqrt{2}\end{matrix}\right.\)
TH1: \(t=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sinx+cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\left(l\right)\\x=k2\pi\left(l\right)\end{matrix}\right.\)
TH2: \(t=-\sqrt{2}\)
\(\Leftrightarrow sinx+cosx=-\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)=-\sqrt{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\pi+k\pi\\x-\dfrac{\pi}{4}=-\pi+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{4}+k\pi\left(tm\right)\\x=-\dfrac{3\pi}{4}+k\pi\left(tm\right)\end{matrix}\right.\)
Vậy ...