Cho f(x) = 1 + x3 + x5 + x7 + ... + x101. Tính f( 1) ; f( -1)
Những câu hỏi liên quan
Cho
f
(
x
)
1
+
x
3
+
x
5
+
x
7
+
.
.
.
.
+
x
101
. Tính f(1); f(-1) A. f(1) 101; f(-1) -100 B. f(1) 51; f(-1...
Đọc tiếp
Cho f ( x ) = 1 + x 3 + x 5 + x 7 + . . . . + x 101 . Tính f(1); f(-1)
A. f(1) = 101; f(-1) = -100
B. f(1) = 51; f(-1) = -49
C. f(1) = 50; f(-1) = -50
D. f(1) = 101; f(-1) = 100
Thay x = 1 vào f(x) ta được
f ( 1 ) = 1 + 1 3 + 1 5 + 1 7 + … + 1 101 = 1 + 1 + 1 + … + 1 ⏟ 51501 = 51.1 = 51
Thay x = -1 vào f(x) ta được
f ( − 1 ) = 1 + ( − 1 ) 3 + ( − 1 ) 5 + ( − 1 ) 7 + … + ( − 1 ) 101 = 1 + ( − 1 ) + ( − 1 ) + … + ( − 1 ) ⏟ 50 : 0 ( − 1 ) = 1 + 50. ( − 1 ) = 1 − 50 = − 49 Vây f ( 1 ) = 51 ; f ( − 1 ) = − 49
Chọn đáp án B
Đúng 0
Bình luận (0)
Câu 5.(1,0 điểm): Cho f(x) 1 + x3 + x5 + x7 + ... + x101. Tính f( 1) ; f( -1)
Đọc tiếp
Câu 5.(1,0 điểm):
Cho f(x) = 1 + x3 + x5 + x7 + ... + x101.
Tính f( 1) ; f( -1)
Cho f(x) 1+x3+x5+x7+...+x51f(x) 1+x3+x5+x7+...+x51. Khi đó f(-1) bằng: A.– 24 B.26 C.– 25 D.– 23
Đọc tiếp
Cho . Khi đó f(-1) bằng:
A.– 24
B.26
C.– 25
D.– 23
X x3;X x5;X x7;...X x101=31200
Cho
f
(
x
)
x
2
+
2
x
3
-
7
x
5
-
9
-
6
x
7
+
x
3
+
x
2
+
x
5
-
4
x
2
+...
Đọc tiếp
Cho
f ( x ) = x 2 + 2 x 3 - 7 x 5 - 9 - 6 x 7 + x 3 + x 2 + x 5 - 4 x 2 + 3 x 7 g ( x ) = x 5 + 2 x 3 - 5 x 8 - x 7 + x 3 + 4 x 2 - 5 x 7 + x 4 - 4 x 2 - x 6 - 12 h ( x ) = x + 4 x 5 - 5 x 6 - x 7 + 4 x 3 + x 2 - 2 x 7 + x 6 - 4 x 2 - 7 x 7 + x
Tính f(x) + g(x) – h(x)
f(x)=1+x3+x5+x7+...+x101
Tính f(1) và f(-1)
Giúp tớ ngay trong tối nay
Giá trị của đa thức x + x3 + x5 + x7 + x9 + ...... + x101 tại x = -1 là:
(A) -101;
(B) -100;
(C) -51;
(D) -50
Hãy chọn phương án đúng.
Thay x = -1 vào biểu thức đã cho ta được:
(-1) + ( -1)3 + (-1)5 + (-1)7 +...+ (-1)101
= (-1) + (-1) + (-1) + (-1) +(- 1)+ ... + (-1) (51 số -1)
= -51.
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho f(x) x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
Đọc tiếp
Cho f(x)= x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) = x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
Đúng 0
Bình luận (0)
Đa thức có bậc là 5 nhe
Cho hàm số
y
f
(
x
)
có đồ thị
f
(
x
)
như hình bên. Biết rằng:
f
(
x
3
)
f
(
x
o
)
và
f
(
x
1
)
+
f
(
x
2
)...
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị f ( x ) như hình bên. Biết rằng: f ( x 3 ) = f ( x o ) và f ( x 1 ) + f ( x 2 ) = f ( x 5 ) + f ( x 7 ) Giá trị lớn nhất của hàm số y = f ( x ) trên [ x 1 ; x 7 ] bằng
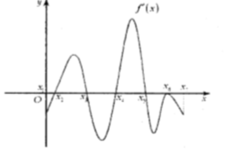
A . f ( x 1 )
B . f ( x 3 )
C . f ( x 5 )
D . f ( x 7 )
