Một quả cầu có khối lượng m = 100g được treo vào đầu dưới của một lò xo có chiều dài tự nhiên l0 = 30cm, độ cứng k = 100N/m, đầu trên cố định. Cho g = 10m/s2. Chiều dài của lò xo ở vị trí cân bằng là:
A. 31cm.
B. 29cm.
C. 20cm.
D. 18cm.
Chọn A
+ lCB = lO + ΔlO = m g k = 0 , 3 + 0 , 1 . 10 100 = 0,31m = 31cm.
Đúng 0
Bình luận (0)
Một lò xo có chiều dài tự nhiên là l0cm. Treo lò xo thẳng đứng và móc vào đầu dưới một quả cân có khối lượng m1 100g, lò xo dài 31cm. Treo thêm vào đầu dưới một quả cân nữa khối lượng m2 100g, nó dài 32cm. Lấy g 10m/s2. Tính độ cứng và chiều dài tự nhiên của lò xo. A. 100N/m; 30cm. B. 100N/m; 29cm. C. 120N/m; 30cm. D. 120N/m; 29cm.
Đọc tiếp
Một lò xo có chiều dài tự nhiên là l0cm. Treo lò xo thẳng đứng và móc vào đầu dưới một quả cân có khối lượng m1 = 100g, lò xo dài 31cm. Treo thêm vào đầu dưới một quả cân nữa khối lượng m2 = 100g, nó dài 32cm. Lấy g = 10m/s2. Tính độ cứng và chiều dài tự nhiên của lò xo.
A. 100N/m; 30cm.
B. 100N/m; 29cm.
C. 120N/m; 30cm.
D. 120N/m; 29cm.
Chọn đáp án A
Ta có: P1 = m1g = k.∆ℓ1
<->0,1.10 = k(0,31 - ℓo) (1)
P2 = (m1 + m2)g = k.∆ℓ2
<-> 0,2.10 = k.(0,32 - ℓo)
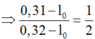
→ ℓo = 0,3m = 30cm.
Thay vào (1)
→ k = 100N/m.
Đúng 0
Bình luận (0)
Treo vào một lò xo có khối lượng 500g vào đầu dưới của lò xo gắn cố định thì thấy lò xo dài 25cm . Tìm chiều dài ban đầu của lò xo. Biết lò xo có độ lớn 100N/m và g= 10m/s^2
Đổi 500 g= 0,5 kg; 25 cm =0,25 m
\(\left|\Delta l\right|=\dfrac{m\cdot g}{k}=\dfrac{0,5\cdot10}{100}=0,05\left(m\right)\)
\(l_0=l'-\left|\Delta l\right|=0,25-0,05=0,2\left(m\right)=20\left(cm\right)\)
Đúng 0
Bình luận (0)
Một quả cầu có khối lượng m 200 g treo vào đầu dưới của một lò xo có chiều dài tự nhiên
l
0
35
c
m
, độ cứng k 100 N/m, đầu trên cố định. Lấy
g
10
m
/
s
2
. Chiều dài lò xo khi vật dao động qua vị trí có vận tốc cực đại? A. 33 cm B. 35 cm C. 39 cm D. 37 cm
Đọc tiếp
Một quả cầu có khối lượng m = 200 g treo vào đầu dưới của một lò xo có chiều dài tự nhiên l 0 = 35 c m , độ cứng k = 100 N/m, đầu trên cố định. Lấy g = 10 m / s 2 . Chiều dài lò xo khi vật dao động qua vị trí có vận tốc cực đại?
A. 33 cm
B. 35 cm
C. 39 cm
D. 37 cm
Khi người ta treo quả cân có khối lượng 300g vào đầu dưới của một lò xo (đầu trên cố định), thì lò xo dài 3 lcm. Khi treo thêm quả cân 200g nữa thì lò xo dài 33cm. Lấy g
10
m
/
s
2
. Chiều dài tự nhiên và độ cứng của lò xo là A. 28cm; 1000N/m B. 30cm; 300N/m C. 32cm; 200N/m D. 28cm; 100N/m
Đọc tiếp
Khi người ta treo quả cân có khối lượng 300g vào đầu dưới của một lò xo (đầu trên cố định), thì lò xo dài 3 lcm. Khi treo thêm quả cân 200g nữa thì lò xo dài 33cm. Lấy g = 10 m / s 2 . Chiều dài tự nhiên và độ cứng của lò xo là
A. 28cm; 1000N/m
B. 30cm; 300N/m
C. 32cm; 200N/m
D. 28cm; 100N/m
Treo vật có khối lượng 400g vào một lò xo có độ cứng 100N/m, lò xo dài 30cm. Lấy g = 10m/s2, chiều dài ban đầu của lò xo là:
A. 25cm
B. 26cm
C. 27cm
D. 28cm
Chọn đáp án B
Ta có:
kΔl = mg
Chiều dài ban đầu của lò xo là:
l0 = l – Δl = 30 – 4 =26 cm
Đúng 0
Bình luận (1)
một lò xo có độ cứng bằng 500N/m được treo thẳng đứng, đầu trên cố định đầu dưới gắn một vật có khối lượng 1kg thì lò xo dài 22cm
a.Tính độ biến dạng của lò xo Δl b.Tính chiều dài tự nhiên lo của lò xo. Lấy g=10m/s2
\(F_{đh}=P=10m=10\cdot1=10N\)
\(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{10}{500}=0,02m=2cm\)
\(l=l_0+\Delta l\Rightarrow l_0=l-\Delta l=22-2=20cm\)
Đúng 1
Bình luận (0)
Một lò xo nhẹ độ cứng k 100N/m, chiều dài tự nhiên l0 20cm. Gắn lò xo vào trần của một toa tàu, đầu dưới của lò xo gắn vào vật có khối lượng m 100g. Cho toa tàu chuyển động nhanh dần đều theo phương ngang a 5,77m/s2 (
10
3
3
m/s2 ). lấy g 10m/s2. Tìm chiều dài của lò xo khi đó. A. 21cm. B. 20,07cm. C. 21,2cm. D. 22,8cm.
Đọc tiếp
Một lò xo nhẹ độ cứng k = 100N/m, chiều dài tự nhiên l0 = 20cm. Gắn lò xo vào trần của một toa tàu, đầu dưới của lò xo gắn vào vật có khối lượng m = 100g. Cho toa tàu chuyển động nhanh dần đều theo phương ngang a = 5,77m/s2 (= 10 3 3 m/s2 ). lấy g = 10m/s2. Tìm chiều dài của lò xo khi đó.
A. 21cm.
B. 20,07cm.
C. 21,2cm.
D. 22,8cm.
Đáp án C.
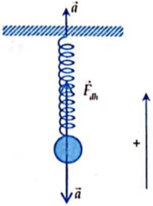
Áp dụng định luật II Niu-tơn cho vật m: F đ h → + P → = m a → (1)
Gọi là góc lệch giữa trục của lò xo và phương thẳng dứng.
Chiếu (1) lên hộ trục Oxy như hình vẽ:
Đúng 0
Bình luận (0)
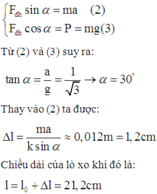
Một lò xo có độ cứng k = 100 N/m có chiều dài tự nhiên là 50 cm. Treo vào đầu dưới của lò xo một vật có khối lượng 0,5 kg, lấy g = 10m/ s 2 . Xác định chiều dài của lò xo khi vật ở vị trí cân bằng.
Tại VTCB ta có:
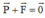→ P = F (1 điểm)
→ mg = k (l – l 0 )
↔ 0,5.10 = 100(l - 0,5)
→ l = 0,55(m) = 55(cm) (1 điểm)
Đúng 0
Bình luận (0)
Lò xo có K = 100N/m, chiều dài tự nhiên l0 = 30cm. Treo vật m = 500g vào đầu dưới của lò xo. Lấy g = 10m/s2. Xác định chiều dài của lò xo khi cân bằng?
<Bạn tự tóm tắt >
Khi cân bằng
Thì \(P=\left|F_{đh}\right|\Rightarrow m\cdot g=K\cdot\left|\Delta l\right|\)
\(\Rightarrow0,5\cdot10=100\cdot\left|\Delta l\right|\Rightarrow\left|\Delta l\right|=0,05\left(m\right)=5\left(cm\right)\)
Chiều dài của lò xo khi cân bằng là
\(l=\left|\Delta l\right|+l_0=5+30=35\left(cm\right)\)
Đúng 1
Bình luận (3)
\(\omega=\sqrt{\dfrac{k}{m}}=......=......\pi\left(\dfrac{rad}{s}\right)\)
\(F_{danhoi}=P\Rightarrow k\Delta l=mg\)
\(\Rightarrow\Delta l=\dfrac{m}{k}g=\dfrac{g}{\omega^2}=......=.....m=.....cm\)
Chiều dài lò xo tại vị trí cân bằng: \(l=l_0+\Delta l=...+.....=....\left(cm\right)\)
Đúng 0
Bình luận (2)