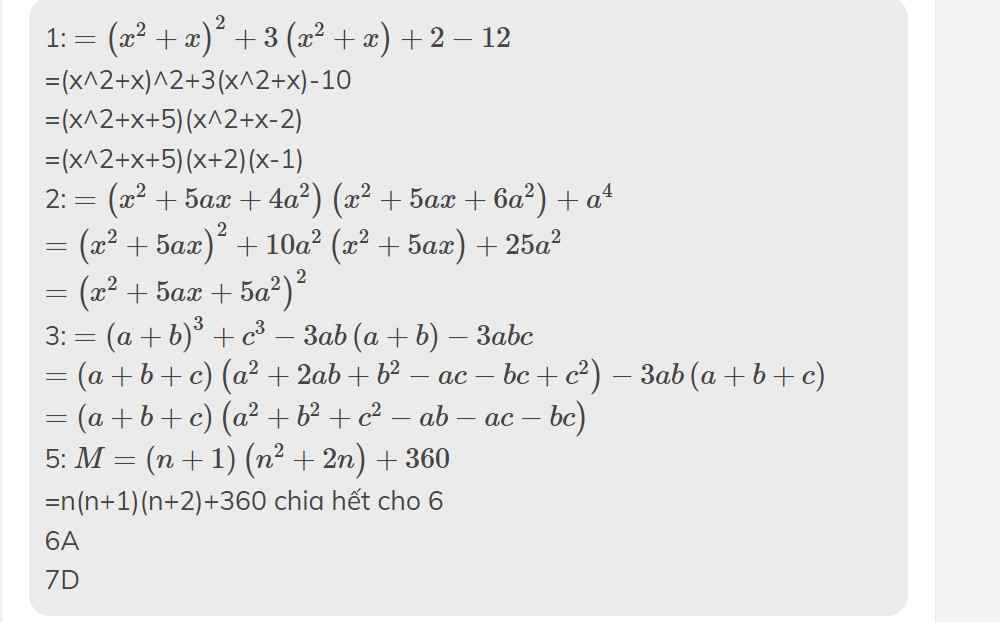Phân tích đa thức sau thành nhân tử: \(\left(x^2+x+1\right)\left(x^2+x+1\right)-12\)

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử (mn giải chi tiết 1 xíu cho mk nhé)
\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(x^2+x+1=t\)
\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12=t\left(t+1\right)-12=t^2+t-12=\left(t^2+t+\dfrac{1}{4}\right)-\dfrac{49}{4}=\left(t+\dfrac{1}{2}\right)^2-\left(\dfrac{7}{2}\right)^2=\left(t+\dfrac{1}{2}-\dfrac{7}{2}\right)\left(t+\dfrac{1}{2}+\dfrac{7}{2}\right)=\left(t-3\right)\left(t+4\right)=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
Đúng 1
Bình luận (0)
\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
= \(\left(x^2+x+1\right)\left[\left(x^2+x+1\right)+1\right]-12\)
= \(\left(x^2+x+1\right)^2\left(x^2+x+1\right)-12\)
= \(\left(x^2+x+1\right)\left(x^2+x+1\right)-3\left(x^2+x+1\right)+4\left(x^2+x+1\right)-4.3\)
= \(\left(x^2+x+1\right)\left(x^2+x-2\right)+4\left(x^2+x-2\right)\)
= \(\left(x^2+x+5\right)\left(x^2+x-2\right)\)
Đúng 1
Bình luận (0)
1) Đa thứcleft(x^2+x+1right)left(X^2+x+2right)-12 được phân tích thành nhân tử là:A)left(x^2+x+5right)left(x+2right)left(x-1right)B)left(x^2+x-5right)left(x+2right)left(x-1right)C)left(x^2-x+5right)left(x+2right)left(x-1right)D)left(x^2+x+5right)left(x-2right)left(x+1right)2) left(x+aright)left(x+2aright)left(x+3aright)left(x+4aright)+a^4 được phân tích thành nhân tử là:A)left(x^2+5ax-5a^2right)left(x^2-5ax+5a^2right)B)left(x^2-5ax-5a^2right)left(x^2+5ax+5a^2right)C)left(x^2-5ax-5a^2right)left(x...
Đọc tiếp
1) Đa thức\(\left(x^2+x+1\right)\left(X^2+x+2\right)\)-12 được phân tích thành nhân tử là:
A)\(\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
B)\(\left(x^2+x-5\right)\left(x+2\right)\left(x-1\right)\)
C)\(\left(x^2-x+5\right)\left(x+2\right)\left(x-1\right)\)
D)\(\left(x^2+x+5\right)\left(x-2\right)\left(x+1\right)\)
2) \(\left(x+a\right)\left(x+2a\right)\left(x+3a\right)\left(x+4a\right)+a^4\) được phân tích thành nhân tử là:
A)\(\left(x^2+5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
B)\(\left(x^2-5ax-5a^2\right)\left(x^2+5ax+5a^2\right)\)
C)\(\left(x^2-5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
D)\(\left(x^2+5ax+5a^2\right)^{^2}\)
3) Đa thức \(a^3+b^3+c^3-3abc\) được phân tích thành nhân tử là:
A)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
B)\(\left(a-b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
C)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
D)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
4) Đa thức x(x+1)(x+2)(x+3)+1 được phân tích thành nhân tử là:
A)\(\left(x^2+3x+1\right)\left(x^2+3x-1\right)\)
B)\(\left(x^2+3x+1\right)^{^2}\)
C)\(\left(x^2+3x+1\right)\left(x^2-3x+1\right)\)
D) Cả B và C đều sai
5) Câu trả lời đúng cho M=\(n^2\left(n+1\right)+2n\left(n+1\right)+360\) với \(n\in Z\)
A)M⋮4
B)M⋮5
C)M⋮6
D)M⋮9
6)Cho \(P=\left(2n+5\right)^{^2}-145\) với \(n\in N\)
A) P⋮4 ; B)P⋮3 ; C) P⋮5 ; D)P⋮6
7) Giá trị của biểu thức \(x^2-y^2-2y-1\) tại
x=502 ; y=497 là:
A) 3000
B)5000
C)4500
D) cả A và B đều sai
Bạn nên tách bài ra để đăng. Không nên đăng 1 loạt như thế này.
Đúng 0
Bình luận (0)
1) Đa thứcleft(x^2+x+1right)left(X^2+x+2right)-12 được phân tích thành nhân tử là:A)left(x^2+x+5right)left(x+2right)left(x-1right)B)left(x^2+x-5right)left(x+2right)left(x-1right)C)left(x^2-x+5right)left(x+2right)left(x-1right)D)left(x^2+x+5right)left(x-2right)left(x+1right) 2) left(x+aright)left(x+2aright)left(x+3aright)left(x+4aright)+a^4 được phân tích thành nhân tử là:A)left(x^2+5ax-5a^2right)left(x^2-5ax+5a^2right)B)left(x^2-5ax-5a^2right)left(x^2+5ax+5a^2right)C)left(x^2-5ax-5a^2right)left(...
Đọc tiếp
1) Đa thức\(\left(x^2+x+1\right)\left(X^2+x+2\right)\)-12 được phân tích thành nhân tử là:
A)\(\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
B)\(\left(x^2+x-5\right)\left(x+2\right)\left(x-1\right)\)
C)\(\left(x^2-x+5\right)\left(x+2\right)\left(x-1\right)\)
D)\(\left(x^2+x+5\right)\left(x-2\right)\left(x+1\right)\)
2) \(\left(x+a\right)\left(x+2a\right)\left(x+3a\right)\left(x+4a\right)+a^4\) được phân tích thành nhân tử là:
A)\(\left(x^2+5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
B)\(\left(x^2-5ax-5a^2\right)\left(x^2+5ax+5a^2\right)\)
C)\(\left(x^2-5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
D)\(\left(x^2+5ax+5a^2\right)^{^2}\)
3) Đa thức \(a^3+b^3+c^3-3abc\) được phân tích thành nhân tử là:
A)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
B)\(\left(a-b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
C)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
D)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
5) Câu trả lời đúng cho M=\(n^2\left(n+1\right)+2n\left(n+1\right)+360\) với \(n\in Z\)
A)M⋮4
B)M⋮5
C)M⋮6
D)M⋮9
6)Cho \(P=\left(2n+5\right)^{^2}-145\) với \(n\in N\)
A) P⋮4 ; B)P⋮3 ; C) P⋮5 ; D)P⋮6
7) Giá trị của biểu thức \(x^2-y^2-2y-1\) tại
x=502 ; y=497 là:
A) 3000
B)5000
C)4500
D) cả A và B đều sai
1: \(=\left(x^2+x\right)^2+3\left(x^2+x\right)+2-12\)
=(x^2+x)^2+3(x^2+x)-10
=(x^2+x+5)(x^2+x-2)
=(x^2+x+5)(x+2)(x-1)
2: \(=\left(x^2+5ax+4a^2\right)\left(x^2+5ax+6a^2\right)+a^4\)
\(=\left(x^2+5ax\right)^2+10a^2\left(x^2+5ax\right)+25a^2\)
\(=\left(x^2+5ax+5a^2\right)^2\)
3: \(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
5: \(M=\left(n+1\right)\left(n^2+2n\right)+360\)
=n(n+1)(n+2)+360 chia hết cho 6
6A
7D
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
\(x^2\left(x+4\right)^2-\left(x+4\right)^2-\left(x^2-1\right)\)
\(x^2\left(x+4\right)^2-\left(x+4\right)^2-\left(x^2-1\right)\)
\(=\left(x+4\right)^2\left(x^2-1\right)-\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left[\left(x+4\right)^2-1\right]\)
\(=\left(x-1\right)\left(x+1\right)\left(x+4+1\right)\left(x+4-1\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x+5\right)\left(x-3\right)\)
=.= hok tốt!!
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử:
\(x^2\left(x^4-1\right)\left(x^2+2\right)+1\)
Ta có :
\(x^2\left(x^4-1\right)\left(x^2+1\right)+1=x^2\left(x^2-1\right)\left(x^2+1\right)\left(x^2+2\right)+1\)
\(\Leftrightarrow x^2\left(x^2+1\right)\left(x^2-1\right)\left(x^2+2\right)+1=\left(x^4-x^2\right)\left(x^4+x^2-2\right)+1\)
Gọi \(x^4-x^2\) là t, ta có:
t(t-2)+1=\(t^2-2t+1=\left(t-1\right)^2=\left(x^4+x^2-1\right)^2\)
Phân tích đa thức sau thành phần tử:
\(a,2x^2-14x\\ b,\left(x^2-2x+1\right):\left(x-1\right)12+5x=8\)
\(a,=2x\left(x-7\right)\\ b,=\left(x-1\right)^2:\left(x-1\right)=x-1\\ c,\Rightarrow5x=8-12=-4\Rightarrow x=-\dfrac{4}{5}\)
Đúng 1
Bình luận (0)
phân tích đa thức sau thành nhân tử: \(\left(x-y\right)^2+4\left(x-y\right)-12\)
\(\left(x^2+x\right)^2+\left(x^2+x+2\right)-12\\ \)
Phân tích đa thức thành nhân tử
Sai đề rồi đa thức này không có nghiêm làm sao phân tích được
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
\(2\left(x^2-6x+1\right)^2+5\left(x^2-6x+1\right)\left(x^2+1\right)+2\left(x^2+1\right)^2\)
Đặt: \(x^2-6x+1=a;x^2+1=b\)
Khi đó đa thức này có dạng:
\(2a^2+5ab+2b^2=2a^2+4ab+ab+2b^2\)
\(=2a\left(a+2b\right)+b\left(a+2b\right)=\left(a+2b\right)\left(2a+b\right)\)
Thay lại a và b thì được:
\(\left(a+2b\right)\left(2a+b\right)=\left(x^2-6x+1+2x^2+2\right)\left(2x^2-12x+2+x^2+1\right)\)
\(=\left(3x^2-6x+3\right)\left(3x^2-12x+3\right)\)
\(=9\left(x-1\right)^2\left(x^2-4x+1\right)\)
Vậy ...
Đúng 0
Bình luận (0)