\(x^3-4x^2+x+6=0\)

\(\Leftrightarrow x^3-5x^2+6x+x^2-5x+6=0\)

\(\Leftrightarrow x\left(x^2-5x+6\right)+\left(x^2-5x+6\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-5x+6\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x-2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}x+1=0\\x-2=0\\x-3=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\x=2\\x=3\end{array}\right.\)

\(3x^3+4x^2+2x+1=0\)

\(\Leftrightarrow\left(3x^3+x^2+x\right)+\left(3x^2+x+1\right)=0\)

\(\Leftrightarrow x\left(3x^2+x+1\right)+1\left(3x^2+x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x^2+x+1\right)=0\)

Ta có:\(3x^2+x+1=3\left(x^2+x.\frac{1}{3}+\frac{1}{3}\right)\)

\(=3\left(x^2+2.x.\frac{1}{6}+\frac{1}{36}-\frac{1}{36}+\frac{1}{3}\right)\)

\(=3\left[\left(x+\frac{1}{6}\right)^2+\frac{11}{36}\right]\ge3.\frac{11}{36}=\frac{11}{12}>0\forall x\)

Do đó x + 1 = 0 tức là x = -1

\(3x^3+3x^2+x^2+x+x+1=0\)

\(3x^2.\left(x+1\right)+x.\left(x+1\right)+\left(x+1\right)=0\)

\(\left(x+1\right).\left(3x^2+x+1\right)=0\)

+)\(3x^2+x+1=0\Leftrightarrow3.\left(x^2+x+\frac{1}{3}\right)=0\Leftrightarrow3.\left(x+\frac{1}{6}\right)^2+\frac{11}{12}=0\left(loai\right)\)

+) x+1=0 <=> x=-1

t sao cl gì v??

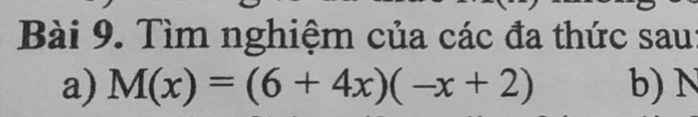
Lời giải:

$M(x)=(6+4x)(-x+2)=0$

\(\Leftrightarrow \left[\begin{matrix} 6+4x=0\\ -x+2=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=-\frac{3}{2}\\ x=2\end{matrix}\right.\)

Vậy nghiệm của đa thức $M(x)$ là $x=\frac{-3}{2}$ và $x=2$

a)g(x)=0=>11x3+5x2+4x+10=0

=>(10x3+10)+(x3+x2)+(4x2+4x)=0

=>10(x3+1)+x2(x+1)+4x(x+1)=0

=>10(x+1)(x2−x+1)+x2(x+1)+4x(x+1)=0

=>(x+1)[(10(x2−x+1)+x2+4x]=0

=>(x+1)(11x2−6x+10)=0

=>(x+1)[(9x2−2.3x+1)+2x2+9]=0

=>(x+1)[(3x−1)2+2x2+9]=0

=>x+1=0

=>x=-1

Vậy x=-1

a) Thay đa thức này bằng 0, ta được: 

f(x) = x^3 - x^2 + x - 1 = 0

=> f(x) = x . x² - x . x + x - 1 = 0

=> f(x) = x. (x² - x + x) = 0 + 1 = 1

=> f(x) = x . x² = 1

=> x = 1   và    x² = 1

=> x = 1

Vậy nghiệm của đa thức là x = 1

Hướng dẫn:

\(\left(m-2\right)x^4-3x^2+m+2=0\left(1\right)\)

TH1:  m - 2 = 0 <=> m = 2 

khi đó phương trình trở thành: \(-3x^2+4=0\)

<=> \(x=\pm\frac{2}{\sqrt{3}}\)

TH2: m khác 2

Đặt: \(x^2=t\ge0\)

Ta có phương trình ẩn t: \(\left(m-2\right)t^2-3t+m+2=0\left(2\right)\)

có: \(\Delta=3^2-4\left(m-2\right)\left(m+2\right)=-4m^2+25\)

+) Phương trình (1)  vô nghiệm <=> phương trình (2) vô nghiệm 

<=> \(\Delta\)<0  ( tự giải ra) 

+) Phương trình (1) có 1 nghiệm <=> phương trình 2 có 1 nghiệm bằng 0 và 1 nghiệm âm ( có thể có hoặc có thể không ) 

+) phương trình (1) có 3 nghiệm <=> phương trình 2 có 1 nghiệm bằng 0 và 1 nghiệm dương

Với t = 0 thay vào ta có: \(\left(m-2\right)0^2-3.0+m+2=0\)

<=> m = - 2 

Thay vào phương trình (2) : \(-4t^2-3.t=0\)

<=> \(t\left(4t+3\right)=0\)

<=> t = 0 

=> Không tồn tại t để phương trình có 3 nghiệm và m = -2 thì phương trình có 1 nghiệm 

+) Phương trình (1) có 2 nghiệm  <=>phuowng trình (2) có 2 nghiệm trái dấu 

<=> m + 2 < 0 <=> m < - 2 

Kết hợp với TH1 nữa nhé!

+)  Phương trình (1) có 4 nghiệm 

<=> phương trình 2 có 2 nghiệm dương 

<=> \(\Delta\ge0;P>0;S>0\) ( tự giải)

4x² + x - 3 = 0

<=> 4x² + 4x - 3x - 3 = 0

<=> 4(x + 1) - 3(x + 1) = 0

<=> (x + 1)(4x - 3) = 0

<=> \(\orbr{\begin{cases}x+1=0\\4x-3=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=-1\\x=\frac{3}{4}\end{cases}}\)

Vậy: x = -1; x = 3/4 là nghiệm của đa thức 4x² + x - 3

\(4x^2+x-3\)

\(4xx+x-3\)

\(x\left(4x+1\right)-3\)

\(x^2-5x+6=0\)

\(x^2-2x-3x+6=0\)

\(x\left(x-2\right)-3\left(x-2\right)=0\)

\(\left(x-3\right)\left(x-2\right)=0\)

                   \(x=3\)

                  \(x=2\)

Vậy x = 3 và x = 2 là nghiệm của đa thức trên. (cái đa thức kia bạn ghi rõ lại hơn đi)