tìm cực trị của hàm số y = (x2+4)/x

Những câu hỏi liên quan
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Cho hàm số y = f (x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x 2 - 4 ) Số điểm cực trị của hàm số y = f(x) là:
A. 4
B. 1
C. 2
D. 3
Tìm tất các giá trị thực của tham số m để hàm số
y
1
3
x
3
+
(
m
+
3
)
x
2
+
4
(
m
+
3
)
x
+
m
3...
Đọc tiếp
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn -2< x 1 < x 2
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
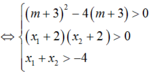
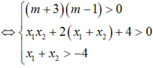
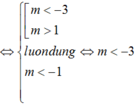
Chọn C
Đúng 0
Bình luận (0)
Tìm tất các giá trị thực của tham số m để hàm số
y
1
3
x
3
+
(
m
+
3
)
x
2
+
4
(
m
+...
Đọc tiếp
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn - 1 < x 1 < x 2
A. - 7 2 < m < - 2 .
B. - 3 < m < 1 .
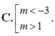
D. - 7 2 < m < - 3 .
Chọn A
![]()
Hàm số có 2 cực trị ⇔ y ' = 0 có hai nghiệm phân biệt x 1 , x 2 thỏa mãn: - 1 < x 1 < x 2
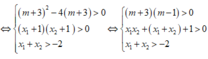
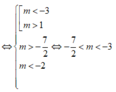
Đúng 0
Bình luận (0)
Cho hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
+
3
)
x
+
m
-
4
. Tìm m để hàm số yf(|x|) có 5 điểm cực trị A. -3m-1 B. m1 C. m4 D. m0
Đọc tiếp
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0
Tìm số điểm cực trị của hàm số
y
x
3
−
x
2
−
x
+
1
. A. n4 B. n2 C. n3 D. n1
Đọc tiếp
Tìm số điểm cực trị của hàm số y = x 3 − x 2 − x + 1 .
A. n=4
B. n=2
C. n=3
D. n=1
Tìm số điểm cực trị của hàm số y = x 3 − x 2 − x + 1
A. n = 4
B. n = 2
C. n = 3
D. n = 1
Đáp án C.
Cách 1: Tập xác định: D = ℝ
Ta có:
y = x 3 − x 2 − x + 1 = x 6 − x 2 − x 2 + 1
⇒ y ' = 6 x 5 2 x 6 − 2 x − 2 x 2 x 2 = 3 x 5 − 2 x x 6 − x . x 4 x 6
Ta thấy y' không xác định tại x=0.
- Nếu x > 0 : y ' = 3 x 2 − 2 x 4 − x 3 x 3 = 3 x 2 − 2 x − 1 ; y ' = 0 ⇒ x = 1 .
- Nếu x < 0 :
y ' = 3 x 5 + 2 x 4 − x 3 − x 3 = − 3 x 2 − 2 x + 1 y ' = 0 ⇒ x = − 1
Bảng biến thiên:
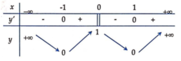
Hàm số đã cho có 3 điểm cực trị.
Cách 2: Đặt t = x , t ≥ 0 . Xét hàm số f t = t 3 − t 2 − t + 1, t ≥ 0 .
Ta có:
f ' t = 3 t 2 − 2 t − 1 ; f ' t = 0 ⇔ t = 0
Bảng biến thiên của hàm số f(t):
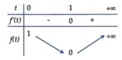
Ta có hàm số y = x 3 − x 2 − x + 1 là hàm số chẵn (đồ thị đối xứng qua trục Oy).
Suy ra bảng biến thiên của hàm số y = x 3 − x 2 − x + 1 :
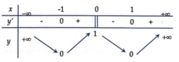
Do đó hàm số y = x 3 − x 2 − x + 1 có 3 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
+
1
)
(
x
2
+
2
m
x
+
4
)
. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số
y
f
(
x
)
2
có đúng một điể...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x + 1 ) ( x 2 + 2 m x + 4 ) . Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y = f ( x ) 2 có đúng một điểm cực trị.
A. 1.
B. 4.
C. 2.
D. 3.
Tìm tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
-
1
)
x
2
+
4
(
m
-
2
)
x
+
2
có hai cực trị
x
1
,
x
2
thỏa mãn
x
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m - 1 ) x 2 + 4 ( m - 2 ) x + 2 có hai cực trị x 1 , x 2 thỏa mãn x 2 1 + x 2 2 + 3 x 1 x 2 = 4
A. m= -2 hoặc m = -1
B. m = -1 hoặc m = 2
C. m = - 1 ± 21
D. Không tồn tại m