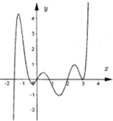
Đáp án C.
Cách 1: Tập xác định: D = ℝ
Ta có:
y = x 3 − x 2 − x + 1 = x 6 − x 2 − x 2 + 1
⇒ y ' = 6 x 5 2 x 6 − 2 x − 2 x 2 x 2 = 3 x 5 − 2 x x 6 − x . x 4 x 6
Ta thấy y' không xác định tại x=0.
- Nếu x > 0 : y ' = 3 x 2 − 2 x 4 − x 3 x 3 = 3 x 2 − 2 x − 1 ; y ' = 0 ⇒ x = 1 .
- Nếu x < 0 :
y ' = 3 x 5 + 2 x 4 − x 3 − x 3 = − 3 x 2 − 2 x + 1 y ' = 0 ⇒ x = − 1
Bảng biến thiên:
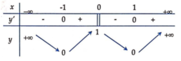
Hàm số đã cho có 3 điểm cực trị.
Cách 2: Đặt t = x , t ≥ 0 . Xét hàm số f t = t 3 − t 2 − t + 1, t ≥ 0 .
Ta có:
f ' t = 3 t 2 − 2 t − 1 ; f ' t = 0 ⇔ t = 0
Bảng biến thiên của hàm số f(t):
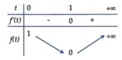
Ta có hàm số y = x 3 − x 2 − x + 1 là hàm số chẵn (đồ thị đối xứng qua trục Oy).
Suy ra bảng biến thiên của hàm số y = x 3 − x 2 − x + 1 :
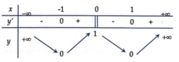
Do đó hàm số y = x 3 − x 2 − x + 1 có 3 điểm cực trị.