Đề sai nhé bạn nếu mà cho tam giác ABC cân tại A thì sẽ có AB=AC=50cm hoặc AB=AC=60 cm ko thể là AB=50 AC=60 nhé bạn :)

Mik viết sai đề nha bạn . đề là :Cho tam giác ABC cân tại A có AB=50cm, BC=60cm. Cac đường cao AD,CE cắt nhau tại H. Tính Ch

a) \(\Delta ABC\) cân nên đường cao AD cũng là trung tuyến => BD = DC = 30 cm
Áp dụng Pitago trong tam giác vuông ADB ta tính được AD = 40 cm
Ta giác vuông ABD ~ CHD (g.g)
=> \(\frac{AB}{CH}=\frac{AD}{CD}\) hay CH = \(\frac{AB.CD}{AD}=\frac{150}{4}\) cm

a: Ta có: ΔABC cân tại A

mà AD là đường cao

nên D là trung điểm củabC

=>BD=CD=30cm

AD=40cm

Xét ΔADC vuông tại D và ΔBEC vuông tại E có

góc C chung

Do đó: ΔADC đồng dạng với ΔBEC

Suy ra: DC/EC=AC/BC=AD/BE

=>30/EC=50/60=40/BE

=>30/EC=40/BE=5/6

=>EC=36cm; BE=48cm

b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có

góc HBD chung

Do đó: ΔBDH đồng dạg với ΔBEC

Suy ra: BH/BC=BD/BE

=>BH/60=30/48=5/8

hay BH=37,5(cm)

=>CH=37,5cm

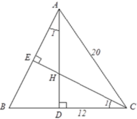
Tam giác ABC cân tại A  nên B D = D C = B C 2 = 24 2 = 12 ( c m )

Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2

Nên AD = 16cm

Xét ΔCDH và ΔADB có:

C D H ^ = A D B ^ = 90 ∘

C 1 = A 1 (cùng phụ với B)

Do đó ΔCDH ~ ΔADB (g.g)

Nên H D B D = H C A B = C D A D , tức là  H D 12 = H C 20 = 12 16 = 3 4

Suy ra HD = 9cm.

Đáp án: C

b: Xét ΔABD vuông tại D và ΔCBE vuông tại E có 

\(\widehat{B}\) chung

Do đó: ΔABD\(\sim\)ΔCBE