Bạn tham khảo

Giải:                                                                           

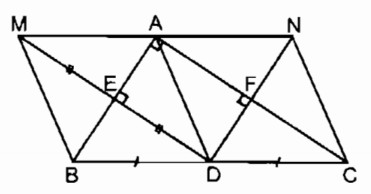
a. Điểm M và điểm D đối xứng qua trục AB

⇒ AB là đường trung trực của đoạn thẳng MD

⇒ AB ⊥ DM

⇒ ˆAED=900AED^=900

Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN

⇒ AC ⊥ DN ⇒ˆAFD=900⇒AFD^=900

ˆEAF=900EAF^=900 (gt)

Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)

b. Tứ giác AEDF là hình chữ nhật ⇒ DE // AC; DF // AB

Trong ∆ ABC ta có: DB = DC (gt)

DE // AC

Suy ra: AE = EB (tính chất đường trung bình tam giác); DF// AB

Suy ra: AF = FC (tính chất đường trung bình của tam giác)

Xét tứ giác ADBM : AE = EB (chứng minh trên)

ED = EM (vì AB là trung trực DM)

Quảng cáo

Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

AB ⊥ DM

Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)

Xét tứ giác ADCN:

AF = FC (chứng minh trên)

DF = FN (vì AC là đường trung trực DN)

Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

AC ⊥ DN

Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)

c. Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD

hay AM // BC và AM = AD (1)

Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN

hay AN // BC và AN = AD (2)

Từ (1) và (2) suy ra: AM trung với AN hay M, A, N thẳng hàng

Và AM = AN  nên A là trung điểm của MN

Vậy điểm M và điểm N đối xứng với nhau qua điểm A

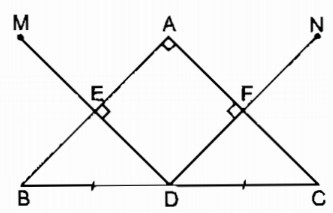
d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF

Ta có: AE = 1212AB ; AF =1212AC

nên AE = AF  AB = AC

Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

a: Xét tứ giác AMIN có

\(\widehat{AIM}=\widehat{AIN}=\widehat{NAM}=90^0\)

Do đó: AMIN là hình chữ nhật

giúp hộ cái mọi người ơi😢

a: Xét tứ giác DMKF có 

KM//DF

KM=DF

Do đó: DMKF là hình bình hành

a/ Xét tứ giác DPMQ có

∠EDF=∠MQD=ˆMPD=90oEDF^=MQD^=MPD^=90o

=> Tứ giác DPMQ là hcn

b/ Để hcn DPMQ là hình vuông thì DM là tia pg ^EDF

c/ Có I đx M qua DE

=> DE là đường t/trực của IM

=> DI = DM (1)

=> t/g DIM cân tại D có DE là đường trung trực

=> DE đồng thời là đường pg

=> ˆIDE=ˆEDMIDE^=EDM^ (2) 

CMTT : DM = DK (3) ; ˆKDF=ˆFDMKDF^=FDM^ (4)

Từ (2) ; (4)

=> ∠IDE+∠EDF+∠KDF=∠IDK=180oIDE^+EDF^+KDF^=IDK^=180o

=> I,D,K thẳng hàng 

Từ (1) ; (3)=> ID = DK

Do đó D là trđ IK

=> I đx K qua D

QDSHYFT

Nhanh hộ mik với