Xét tính chẵn lẻ của hàm số sau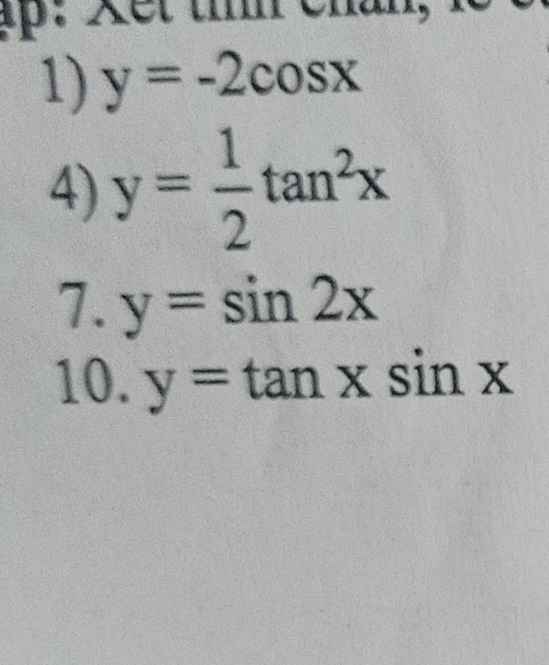

Những câu hỏi liên quan
Xét tính xét tính chẵn lẻ của hàm số sau y = x - sin x
Đặt `y=f(x)=x-sinx`
Có: `f(-x)=-x-sin(-x)=-x+sinx=-(x-sinx)=-f(x)`
`=>` Hàm lẻ.
Đúng 1
Bình luận (0)
Xét tính chẵn lẻ của hàm số sau
2) TXĐ: \(D=R\Rightarrow\forall x\in R\) thì \(-x\in R\)
\(y=f\left(x\right)=sinx+x\)
\(\Rightarrow f\left(-x\right)=sin\left(-x\right)+\left(-x\right)=-sinx-x=-\left(sinx+x\right)=-f\left(x\right)\)
\(\Rightarrow\)\(y=sinx+x\) là hàm lẻ
5) TXĐ: \(D=R\Rightarrow\forall x\in R\) thì \(-x\in R\)
\(y=f\left(x\right)=sin\left|x\right|+x^2\)
\(\Rightarrow f\left(-x\right)=sin\left|-x\right|+\left(-x\right)^2=sin\left|x\right|+x^2=f\left(x\right)\)
\(\Rightarrow y=sin\left|x\right|+x^2\) là hàm chẵn
8) TXĐ: \(D=R\Rightarrow\forall x\in R\) thì \(-x\in R\)
\(y=f\left(x\right)=-2+3cosx\)
\(\Rightarrow f\left(-x\right)=-2+3cos\left(-x\right)=-2+3cosx=f\left(x\right)\)
\(\Rightarrow y=-2+3cosx\) là hàm chẵn
11) TXĐ:\(D=R\Rightarrow\forall x\in R\) thì \(-x\in R\)
\(y=f\left(x\right)=cosx-sin\left|x\right|\)
\(\Rightarrow f\left(-x\right)=cos\left(-x\right)-sin\left|-x\right|=cosx-sin\left|x\right|=\)\(f\left(x\right)\)
\(\Rightarrow y=cosx-sin\left|x\right|\) là hàm chẵn
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau:
Đọc tiếp
Xét tính chẵn lẻ của các hàm số sau:
`y=f(x)=1/(x.cos3x)`
`f(-x)=1/(-x.cos(-3x))=-1/(x.cos3x)=-f(x)`
`=>` Lẻ.
.
`y=f(x)=(cos^3x+1)/(sin^3x)`
`f(-x)=((cos(-x))^3+1)/((sin(-x))^3)=(-cos^3x-1)/(sin^3x)=-f(x)`
`=>` Lẻ.
Đúng 1
Bình luận (0)
xét tính chẵn lẻ của hàm số sau: y=x3 - 5x
TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ
Đúng 3
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = |x|
Đặt y = f(x) = |x|.
+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.
+ f(–x) = |–x| = |x| = f(x).
Vậy hàm số y = |x| là hàm số chẵn.
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = x3 + x
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau :
y = -2x4 + x2 –10
TXĐ: D=R
Nếu \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-2\cdot\left(-x\right)^4+\left(-x\right)^2-10\)
\(=-2x^4+x^2-10\)
=f(x)
=>f(x) là hàm số chẵn
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = (x + 2)2
Đặt y = f(x) = (x + 2)2.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ (x + 2)2 = f(x)
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ – (x + 2)2 = –f(x).
Vậy hàm số y = (x + 2)2 không chẵn, không lẻ.
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = x2 + x + 1
Đặt y = f(x) = x2 + x + 1.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
Vậy hàm số y = x2 + x + 1 không chẵn, không lẻ.
Đúng 0
Bình luận (0)














