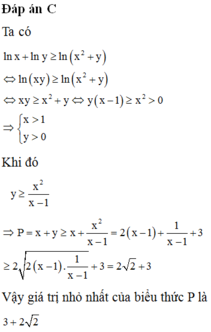cho x,y dương; x+y<1. tìm GTNN: T=1/x^2+xy + 1/y^2+xy

Những câu hỏi liên quan
a)Tìm các số nguyên dương x, y thỏa mãn x+3 chia hết cho y, y+3 chia hết cho x
b)Tìm các số nguyên dương x, y thỏa mãn xy+x+y+2 chia hết cho cả x và y.
cho x y là hai số nguyên dương và y là số âm hỏi y là số nguyên dương hay số nguyên âm nếu : a)x,y là số nguyên dương b)x y là số nguyên âm
a, y là số nguyên âm nếu x,y là số nguyên dương
b,y là số nguyên dương nếu x,y là số nguyên âm
bạn k cho mk nha
cho x,y dương ,tìm gtnn của x/y+y/x+xy/(x+y)
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P x + y A. P 6 B. P
2
+
3
2
C. P
3
+
2
2
D. P
17
+
3
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P = x + y
A. P = 6
B. P = 2 + 3 2
C. P = 3 + 2 2
D. P = 17 + 3
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
ln
x
+
ln
y
≥
ln
(
x
2
+
y
)
là các số thực dương thỏa mãn
P
x
+
y
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln ( x 2 + y ) là các số thực dương thỏa mãn P = x + y
![]()
![]()
![]()
![]()
cho x dương, y dương và \(x^2+y^2=1\)
tìm giá trị lớn nhất của x+y+2(x+y)
Áp dụng BĐT :
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)\)
Đúng 0
Bình luận (1)
sai đề.
sửa lại:
cho x dương, y dương và \(x^2+y^2=1\)
tìm giá trị lớn nhất của\(x+y+2\left(x+y\right)^2\)
Đúng 0
Bình luận (0)
Cho X=(1;4+m], Y=(m;dương vô cực). Tìm m sao cho:
a) X là con Y
b) X giao Y bằng rỗng
c) X hợp Y=(1;dương vô cự
a) X là con Y <=> m< 1
b) X giao Y bằng rỗng <=> m> 4+m <=> không có giá trị m thỏa mãn
c) X hợp Y = (1; dương vô cùng) <=> m=1
Đúng 0
Bình luận (0)
Cho x,y la các sô dương va x+y=1. tìm gia tri nho nhật cua điêu thức p=a^2/x+b^2/y (a va b la hăng sô dương đa cho)
Tìm các số nguyên dương x và y sao cho x^y=y^x
a) tìm số nguyên dương x sao cho x/9<7/x<x/6
b) tìm số nguyên dương y sao cho 3/y<y/7<4/y
MIK CẦN GẤP .MONG MN GIÚP BÀI NÀY KIỂM TRA
a) tìm số nguyên dương x sao cho x/9<7/x<x/6
x/9<7/x
->x^2 <63
7/x<x/6
-> x^2> 42
x/9<x/6
-> x=7 (x là số nguyên dương)
b) tìm số nguyên dương y sao cho 3/y<y/7<4/y
3/y< y/7
-> y^2 >21
y/7 <4/y
-> y^2< 28
-> y= 5 (y là số nguyên dương)