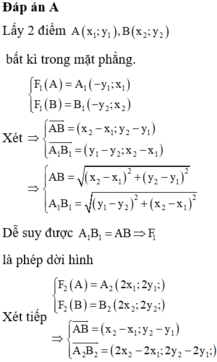Điểm M (x;y)thuộc đường thẳng y= 2x+1 và cách trục hoành một khoảng = 3 . Tìm toạn độ điểm M

Những câu hỏi liên quan
Cho hàm số f(x){left{{}begin{matrix}dfrac{x2}{x};x 1;xne00;x0sqrt{x};xge1end{matrix}right.
Chọn khẳng định đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn [0;1]
B. Hàm số liên tục tại mọi điểm trừ điểm x0
C. Hàm số liên tục tại mọi điểm thuộc R
D. Hàm số liên tục tại mọi điểm trừ điểm x1
Mọi người giúp dùm mình câu này với ạ! Tks nhiều ạ!
Đọc tiếp
Cho hàm số f(x)={\(\left\{{}\begin{matrix}=\dfrac{x2}{x};x< 1;x\ne0\\=0;x=0\\=\sqrt{x};x\ge1\end{matrix}\right.\)
Chọn khẳng định đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn [0;1] B. Hàm số liên tục tại mọi điểm trừ điểm x=0 C. Hàm số liên tục tại mọi điểm thuộc R D. Hàm số liên tục tại mọi điểm trừ điểm x=1 Mọi người giúp dùm mình câu này với ạ! Tks nhiều ạ!
Bạn viết lại công thức của $f(x)$ trường hợp \(x<1, x\neq 0\) hộ mình với
Đúng 0
Bình luận (1)
Xét hai phép biến hình sau: (i) Phép biến hình F1, biến mỗi điểm M(x;y) thành điểm M(-y;x) (ii) Phép biến hình F2 biến mỗi điểm M(x;y) thành điểm M(2x;2y) Phép biến hình nào trong hai phép biến hình trên là phép dời hình? A. Chỉ phép biến hình (i) B. Chỉ phép biến hình (ii) C. Cả hai phép biến hình (i) và (ii) D. Cả hai phép biến hình (i) và (ii) đều không là phép dời hình
Đọc tiếp
Xét hai phép biến hình sau:
(i) Phép biến hình F1, biến mỗi điểm M(x;y) thành điểm M'(-y;x)
(ii) Phép biến hình F2 biến mỗi điểm M(x;y) thành điểm M'(2x;2y)
Phép biến hình nào trong hai phép biến hình trên là phép dời hình?
A. Chỉ phép biến hình (i)
B. Chỉ phép biến hình (ii)
C. Cả hai phép biến hình (i) và (ii)
D. Cả hai phép biến hình (i) và (ii) đều không là phép dời hình
Hàm số \(y=x-\cos2x+2017\)
A. Nhận \(x=\dfrac{-\pi}{12}\) làm điểm cực đại
B. Nhận điểm \(x=\dfrac{-5\pi}{12}\) làm điểm cực tiểu
C. Nhận \(x=\dfrac{7\pi}{12}\) làm điểm cực đại
D. Nhận \(x=\dfrac{11\pi}{12}\) làm điểm cực đại
B. nhận điểm \(x=\dfrac{-5\pi}{12}\) làm điểm cực tiểu
Đúng 1
Bình luận (0)
Cho điểm M( x ; y) có :
x
-
1
+
2
cos
t
y
2
-
2
sin
t
(...
Đọc tiếp
Cho điểm M( x ; y) có :
x = - 1 + 2 cos t y = 2 - 2 sin t ( t ∈ ℝ )
Tập hợp điểm M là:
A. Đường tròn tâm I( 1 ; -2) , bán kính R= 2.
B. Đường tròn tâm I( -1 ;2) , bán kính R= 2.
C. Đường tròn tâm I( -1 ; 2), bán kính R= 4.
D. Đường tròn tâm I( 1; -2) , bán kính R= 4.
Đáp án B
Ta có:
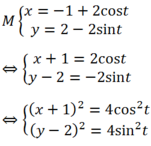
=> ( x +1) 2+ (y- 2) 2= 4cos2t + 4sin2t
=> ( x +1) 2+ (y- 2) 2 = 4
Vậy tập hợp điểm M là phương trình đường tròn có tâm I( -1;2) , bán kính R= 2.
Đúng 0
Bình luận (0)
Trên mặt phảng tọa độ : a) Mỗi điểm M xác định ......... ( x0 ; y0 ) . Ngược lại , mỗi cặp số ( x0 ; y0 ) ........... điểm M .b) Cặp số ( x0 ; y0 ) là tọa độ của điểm m , x0 là ........... và y0 là ........... của điểm M .c) Điểm M có tọa độ .......... đc kí hiệu là M ( x0 , y0 ) .
Đọc tiếp
Trên mặt phảng tọa độ :
a) Mỗi điểm M xác định ......... ( x0 ; y0 ) . Ngược lại , mỗi cặp số ( x0 ; y0 ) ........... điểm M .
b) Cặp số ( x0 ; y0 ) là tọa độ của điểm m , x0 là ........... và y0 là ........... của điểm M .
c) Điểm M có tọa độ .......... đc kí hiệu là M ( x0 , y0 ) .
a,
b,hoành độ,tung độ
c,\(\left(x_0,y_0\right)\)
Đúng 0
Bình luận (0)
tìm m để pt có 3 nghiệm pb : \(4x^3-6x^2+m=0\)
tìm m ? thì y=\(\dfrac{x-3}{x+1}\) cắt y=x+m tại 2 điểm phân biệt
m? thì y=\(\dfrac{x+1}{x-1}\), y=-2x+m cắt tại 2 điểm phân biệt
1.
\(4x^3-6x^2+m=0\Leftrightarrow4x^3-6x^2=-m\)
Xét hàm \(f\left(x\right)=4x^3-6x^2\)
\(f'\left(x\right)=12x^2-12x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
BBT:
Từ BBT ta thấy đường thẳng \(y=-m\) cắt \(y=4x^3-6x^2\) tại 3 điểm pb khi:
\(-2< -m< 0\Leftrightarrow0< m< 2\)
Đúng 2
Bình luận (0)
2.
Pt hoành độ giao điểm:
\(\dfrac{x-3}{x+1}=x+m\)
\(\Rightarrow x-3=\left(x+m\right)\left(x+1\right)\)
\(\Leftrightarrow x^2+mx+m+3=0\) (1)
Đường thẳng cắt đồ thị tại 2 điểm pb khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=m^2-4\left(m+3\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}m>6\\m< -2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.
Pt hoành độ giao điểm:
\(\dfrac{x+1}{x-1}=-2x+m\)
\(\Leftrightarrow x+1=\left(x-1\right)\left(-2x+m\right)\)
\(\Leftrightarrow2x^2-\left(m+1\right)x+m+1=0\) (1)
bài toán thỏa mãn khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+1\right)^2-8\left(m+1\right)>0\)
\(\Leftrightarrow\left(m+1\right)\left(m-7\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}m>7\\m< -1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho hàm số: y= x^3 - 2(m+1)x^2 + (5m+1)x -2m -2 (Cm). Tìm m để (Cm) cắt Ox tại 3 điểm phân biệt A(2;0), B, C sao cho 2 điểm B và C có 1 điểm nằm trong và 1 điểm nằm ngoài đường tròn: x^2 + y^2 = 1
Xem chi tiết
Lời giải:
PT hoành độ giao điểm:
\(x^3-2(m+1)x^2+(5m+1)x-2m-2=0\)
\(\Leftrightarrow (x-2)(x^2-2mx+m+1)=0\)
Vì \(A(2,0)\) nên hoành độ hai điểm \(B,C\) sẽ là nghiệm của PT \(x^2-2mx+m+1=0\)
Điều kiện: \(\Delta'=m^2-(m+1)>0\)
Khi đó, áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của PT thì \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+1\end{matrix}\right.\)
Nhận thấy hai điểm $B,C$ nằm trên $Ox$ mà một điểm nằm trong đường tròn \(x^2+y^2=1\) nên \((x_1-1)(x_2-1)<0\)
\(\Leftrightarrow x_1x_2-(x_1+x_2)+1<0\Leftrightarrow m+1-2m+1<0\)
\(\Leftrightarrow m>2\). Thử lại ta thấy thỏa mãn điều kiện \(\Delta'\)
Vậy \(m>2\)
Đúng 0
Bình luận (0)
Cho (P) y=x2 và (d) y=2x+m
a) Xác định m để (P) và (d)
+ Tiếp xúc nhau. Tìm tiếp điểm
+ Cắt nhau tại A, B và 1 điểm có hoành độ x=-1. Tìm tọa độ A,B
b) Giả sử (d) và (P) cắt nhau tại 2 điểm M, N. Tìm tọa độ trung điểm I của MN. Tìm quỹ tích điểm I
Cho tam giác ABC, trung tuyến BD và CE. Gọi M là điểm đ/x của B qua D, N là điểm đ/x của C qua E. Chứng minh : M là điểm đ/x của N qua điểm A.
Câu 3 (2,0 điểm): Cho hàm số bậc nhất y = (m + 1)x - 3 (với x là biến số )
3.1. (0,5 điểm) Tìm m để đồ thị hàm số trên đi qua điểm (-1;1). 3.2. (1,0 điểm) Tìm m để đồ thị hàm số trên song song với đường thẳng y = - x + 3
(3.3) (0,5 điểm) Gọi A, B lần lượt là giao điểm của đồ thị hàm số với các trục Ox, Oy. Tìm m để tam giác OAB vuông cân.
1:
Thay x=-1 và y=1 vào y=(m+1)x-3, ta được:
-m-1-3=1
=>m+4=-1
=>m=-5
2: Để hai đường song song thì m+1=-1
=>m=-2
3: Tọa độ A là:
y=0 và x=3/m+1
Tọa độ B là:
x=0 và y=-3
=>OA=3/|m+1|; OB=3
Để ΔOAB vuông cân tại O thì OA=OB
=>|m+1|=3/3=1
=>m+1=1 hoặc m+1=-1
=>m=-2 hoặc m=0
Đúng 0
Bình luận (0)