Cho x+y+z=6 và xy+yz+zx=9.CMR: 0<=x<=4/3

Những câu hỏi liên quan
cho x+y+x=0 xy+yz+zx=0 cmr x=y=z
Theo đề: x+y+z=0
=> (x+y+z)2=0
<=> x2+y2+z2 +2xy+2xz+2yz=0
<=> x2 + y2 + z2 + 2.(xy+xz+yz)=0
mà xy+xz+yz=0
=> x2 + y2 +z2 =0
<=> x=y=z=0 (đpcm)
Đúng 0
Bình luận (0)
Cho x,y,z > 0 ; x + y + z = 1
CMR: \(\sqrt{\frac{xy}{z+xy}}+\sqrt{\frac{yz}{x+yz}}+\sqrt{\frac{zx}{y+zx}}\le\frac{3}{2}\)
cho x-y+z=0. CMR xy+yz-zx=0
cho x,y,z thuộc Q* và x-y+z=0. cmr xy+yz-zx>=0
Cho x, y, z >0 thỏa mãn x + y + z = 1
CMR: \(\sqrt{\dfrac{xy}{xy+z}}+\sqrt{\dfrac{yz}{yz+x}}+\sqrt{\dfrac{zx}{zx+y}}\le\dfrac{3}{2}\)
Lời giải:
Áp dụng BĐT AM-GM:
\(\sqrt{\frac{xy}{xy+z}}=\sqrt{\frac{xy}{xy+z(x+y+z)}}=\sqrt{\frac{xy}{(z+x)(z+y)}}\leq \frac{1}{2}\left(\frac{x}{x+z}+\frac{y}{z+y}\right)\)
Hoàn toàn tương tự với các phân thức còn lại suy ra:
\(\sum \sqrt{\frac{xy}{xy+z}}\leq \frac{1}{2}\left(\frac{x+z}{x+z}+\frac{y+z}{y+z}+\frac{x+y}{x+y}\right)=\frac{3}{2}\)
Ta có đpcm.
Dấu "=" xảy ra khi $x=y=z=\frac{1}{3}$
Đúng 0
Bình luận (0)
Cho x, y, z > 0 và x+y+z=1.
CMR : \(\dfrac{1-x^2}{x+yz}+\dfrac{1-y^2}{y+zx}+\dfrac{1-z^2}{z+xy}\ge6\)
Cho các số dương x;y;z. CMR:
\(\dfrac{xy}{x^2+yz+zx}+\dfrac{yz}{y^2+zx+xy}+\dfrac{zx}{z^2+xy+yz}\le\dfrac{x^2+y^2+z^2}{xy+yz+zx}\)
cho x,y,z>0 và x+y+z=1 chứng minh\(\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\ge1+\sqrt{xy}\sqrt{yz}+\sqrt{zx}\)
Cho x,y,z>0 và xy+yz+zx=9. Tìm MaxP=x^5/y^3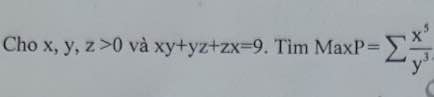
Nếu biểu thức là: \(P=\dfrac{x^5}{y^3}+\dfrac{y^5}{z^3}+\dfrac{z^5}{x^3}\) thì đề bài sai
Biểu thức này chỉ có min, không có max
Đúng 0
Bình luận (1)












