ĐKXĐ: \(x\ne\left\{-4;-5;-6;-7\right\}\)

\(\dfrac{1}{x^2+9x+20}+\dfrac{1}{x^2+11x+30}+\dfrac{1}{x^2+13x+42}=\dfrac{1}{18}\)

\(\Leftrightarrow\dfrac{1}{\left(x+4\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+6\right)}+\dfrac{1}{\left(x+6\right)\left(x+7\right)}=\dfrac{1}{18}\)

\(\Leftrightarrow\dfrac{1}{x+4}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+6}+\dfrac{1}{x+6}-\dfrac{1}{x+7}=\dfrac{1}{18}\)

\(\Leftrightarrow\dfrac{1}{x+4}-\dfrac{1}{x+7}=\dfrac{1}{18}\)

\(\Leftrightarrow\dfrac{3}{\left(x+4\right)\left(x+7\right)}=\dfrac{1}{18}\)

\(\Rightarrow\left(x+4\right)\left(x+7\right)=54\)

\(\Leftrightarrow x^2+11x-26=0\)

\(\Leftrightarrow x^2-2x+13x-26=0\)

\(\Leftrightarrow x\left(x-2\right)+13\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+13\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-13\end{matrix}\right.\)

               Để olm giúp em em nhé!

a,   \(\dfrac{x+2}{7x+42}\) = \(\dfrac{x+2}{7.\left(x+6\right)}\) = \(\dfrac{\left(x+2\right)\left(x-6\right)}{7\left(x-6\right)\left(x+6\right)}\) (đk \(x\ne\) \(\mp\) 6)

 \(\dfrac{-13x}{x^2-36}\) = \(\dfrac{-13x}{\left(x-6\right)\left(x+6\right)}\) = \(\dfrac{-7.13.x}{7.\left(x-6\right).\left(x+6\right)}\) = \(\dfrac{-91x}{7.\left(x-6\right)\left(x+6\right)}\)

b, \(\dfrac{7}{4x+16}\) = \(\dfrac{7\left(x-4\right)}{4.\left(x+4\right).\left(x-4\right)}\) (đk \(x\ne\) \(\pm\) 4)

     \(\dfrac{15}{x^2-16}\) = \(\dfrac{15.4}{\left(x-4\right)\left(x+4\right).4}\) = \(\dfrac{60}{4.\left(x-4\right).\left(x+4\right)}\)

c, \(\dfrac{12}{x^2-4}\) = \(\dfrac{12}{\left(x-2\right).\left(x+2\right)}\)  Đk \(x\) \(\ne\)  \(\pm\) 2

    \(\dfrac{2}{x-3}\) đk \(x\) \(\ne\) 3

\(\dfrac{12}{x^2-4}\) = \(\dfrac{12.\left(x-3\right)}{\left(x^2-4\right).\left(x-3\right)}\) = \(\dfrac{12x-36}{\left(x^2-4\right).\left(x-3\right)}\)

   \(\dfrac{2}{x-3}\) =  \(\dfrac{2.\left(x^2-4\right)}{\left(x-3\right).\left(x^2-4\right)}\) 

\(x^3+6x^2-13x-42=0\)

\(\Leftrightarrow\left(x^3-3x^2\right)+\left(9x^2-27x\right)+\left(14x-42\right)=0\)

\(\Leftrightarrow x^2\left(x-3\right)+9x\left(x-3\right)+14\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)+\left(x^2+9x+14\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x^2+7x+2x+14\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left[x\left(x+7\right)+2\left(x+7\right)\right]=0\)

\(\Leftrightarrow\left(x-3\right)\left(x+2\right)\left(x+7\right)=0\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}x-3=0\\x+2=0\\x+7=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=3\\x=-2\\x=-7\end{array}\right.\)

x³ + 6x² - 13x - 42 = 0

=> x³ - 3x² + 9x² - 27x + 14x - 42 = 0

=> x² ( x - 3 ) + 9x ( x - 3 ) + 14 ( x - 3 ) = 0

=> ( x - 3 ) ( x² + 9x + 14) = 0

=> ( x - 3 ) ( x² + 2x + 7x + 14 ) = 0

=> ( x - 3 ) [ x ( x + 2 ) + 7 ( x + 2 ) ] = 0

=> ( x - 3 ) ( x + 2 ) ( x + 7 ) = 0

=> x - 3 = 0 => x = 3

=> x + 2 = 0 => x = -2

=> x + 7 = 0 => x = -7

Ta có

3 x 2   +   13 x   +   10   =   0     ⇔   3 x 2   +   3 x   +   10 x   +   10   =   0

ó 3x(x + 1) + 10(x + 1) = 0

ó (x + 1)(3x + 10) = 0

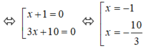
=> 2 x 1 x 2 =   2 . ( - 1 ) . - 10 3 = 20 3

Đáp án cần chọn là: B

Gọi nghiệm của phương trình (2) là x₀ (x₀ ≠ 0)

thì nghiệm phương trình (1) là 2x₀

Thay x₀; 2x₀ lần lượt vào phương trình (2) và (1)

ta được

2 x 0 2 − 13.2 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0

⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0 ⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 4 x 0 2 − 16 x 0 + 4 m = 0

⇔ 10x₀ = −2m ⇔ x 0 = − m 5

Do x₀ ≠ 0 nên m ≠ 0

Thay x 0 = − m 5 vào phương trình (2)

ta được − m 5 2 − 4. − m 5 + m = 0

⇔ m 2 25 + 4 m 5 + m = 0

⇔ m 2 25 + 9 m 5 = 0 ⇒ m = 0 m = − 45

Kết hợp m ≠ 0 ta được m = −45

Đáp án cần chọn là: A

bạn vừa đăng câu này r mà

a: Ta có: \(\left(2x-3\right)^2+6\left(2x-1\right)=7\)

\(\Leftrightarrow\left(2x-3\right)^2+6\left(2x-1\right)-7=0\)

\(\Leftrightarrow4x^2-12x+9+12x-6-7=0\)

\(\Leftrightarrow4x^2=4\)

\(\Leftrightarrow x^2=1\)

hay \(x\in\left\{1;-1\right\}\)

b: Ta có: \(x^2-7x+10=0\)

\(\Leftrightarrow\left(x-5\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)

bạn học sd máy tính tìm nghiệm chưa?

a) \(\left(2x-3\right)^2+6\left(2x-1\right)=7\\ \Rightarrow4x^2-12x+9+12x-6-7=0\\ \Rightarrow4x^2-4=0\\ \Rightarrow x^2-1=0\\ \Rightarrow x^2=1\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)

b) \(x^2-7x+10=0\\ \Rightarrow\left(x^2-2x\right)-\left(5x-10\right)=0\\ \Rightarrow\left(x-2\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

c) \(-6x^2+13x-5=0\\ \Rightarrow-\left(6x^2-13x+5\right)=0\\ \Rightarrow-\left[\left(6x^2-10x\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left[2x\left(3x-5\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left(2x-1\right)\left(3x-5\right)=0\)

    \(\Rightarrow\left[{}\begin{matrix}-\left(2x-1\right)=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x-1=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{5}{3}\end{matrix}\right.\)

d) \(x^4+7x^2-18=0\\ \Rightarrow\left(x^4-4\right)+\left(7x^2-14\right)=0\\ \Rightarrow\left(x^2-2\right)\left(x^2+2\right)+7\left(x^2-2\right)=0\\ \Rightarrow\left(x^2-2\right)\left(x^2+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2-2=0\\x^2+9=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x^2=-9\left(loại\right)\end{matrix}\right.\)

Theo hệ thức Vi-ét ta có:  x 1  +  x 2  =13

Suy ra 12,5 +  x 2  = 13 ⇔  x 2  = 0,5

Cũng theo hệ thức Vi-ét ta có:  x 1 x 2  = m

Suy ra: m = 12,5.0,5 ⇔ m =6,25

Vậy với m = 6,25 thì phương trình  x 2  -13x + m = 0 có hai nghiệm

x 1  =12,5 , x 2  =0,5