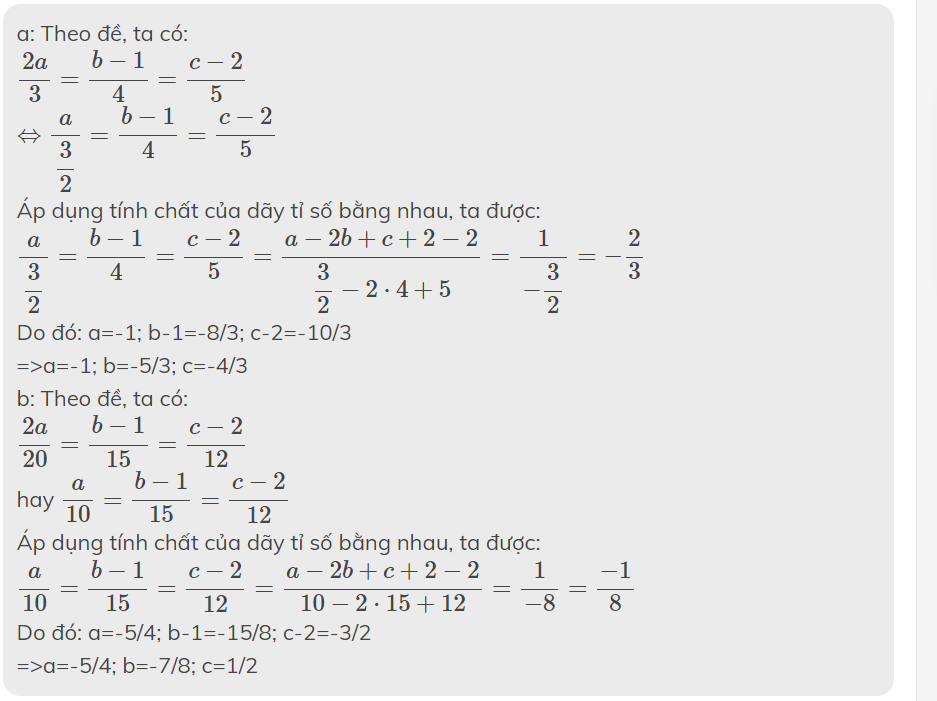Cho a+b=1. Tính A= a^2(2a-3) + b^2(-3+2b)

Những câu hỏi liên quan
cho |a| khác |b| và ab khác 0 thoả mãn (a−b)/(a^2+ab) + (a+b)/(a^2−ab) = (3a−b)/(a^2−b^2).Tính B=(a^3+2a^2b+3b^2)/(2a^3+a^2b+b^3)
cho |a| khác |b| và ab khác 0 thoả mãn (a−b)/(a^2+ab) + (a+b)/(a^2−ab) = (3a−b)/(a^2−b^2).Tính B=(a^3+2a^2b+3b^2)/(2a^3+a^2b+b^3)
Cho a+b=1. Tính giá trị biểu thức: A=a^2(2a-3)+b^2(-3+2b)
\(A=a^2\left(2a-3\right)+b^2\left(-3+2b\right)\)
\(=2a^3-3a^2-3b^2+2b^3\)
\(=2\left(a^3+b^3\right)-3a^2-3b^2\)
\(=2\left(a+b\right)\left(a^2-ab+b^2\right)-3a^2-3b^2\)
\(=2\left(a^2-ab+b^2\right)-3a^2-3b^2\)(vì a + b = 1)
\(=2a^2-2ab+2b^2-3a^2-3b^2\)
\(=-a^2-2ab-b^2=-\left(a^2+2ab+b^2\right)\)
\(=-\left(a+b\right)^2=-1^2=-1\)(vì a + b = 1)
a) Biết 2a, b - 1, c - 2 Tỉ Lệ với 3, 4, 5 và a - 2b + c. Tính a, b, c
b) Biết 2a, b - 1, c - 2 Tỉ Lệ Nghịch 3, 4, 5 và a - 2b + c. Tính a, b, c
Cho a >b . Chứng minh : a)4a – 3 > 4b – 3; b) 1 – 2a < 1- 2b ; c) 5( a+ 3) - 4 > 5( b + 3) – 4; d)5 – 2a < 5 – 2b e) – 2 (1 – a) – 6 > -2 (1 – b ) – 6
a. Ta có: a > b
4a > 4b ( nhân cả 2 vế cho 4)
4a - 3 > 4b - 3 (cộng cả 2 vế cho -3)
b. Ta có: a > b
-2a < -2b ( nhân cả 2 vế cho -2)
1 - 2a < 1 - 2b (cộng cả 2 vế cho 1)
d. Ta có: a < b
-2a > -2b ( nhân cả 2 vế cho -2)
5 - 2a > 5 - 2b (cộng cả 2 vế cho 5)
Đúng 2
Bình luận (1)
bài 1: Cho : x+y= 3 . tính giá trị biểu thức:
A= x^2+2xy+y^2= 4x-4y+1
bài 2:cho a^2+b^2+c^2= m. tính giá trị biểu thức :
B= (2a+2b-c)^2+(2b+2c-a)^2+(2c+2a-b)^2
Cho 2 số thực a,b thỏa mãn: lal khác lbl va ab khac 0 thoa man \(\frac{a-b}{a^2+ab}+\frac{a+b}{a^2-ab}=\frac{3a-b}{a^2-b^2}\)
Tính P=\(\frac{a^3+2a^2b+2b^3}{2a^3+ab^2+2b^3}\)
\(A=\left(\dfrac{1}{2a-b}-\dfrac{a^2-1}{2a^3-b+2a-a^2b}\right)\div\left(\dfrac{4a+2b}{a^3b+ab}-\dfrac{2}{a}\right)\)
a) rút gọn biểu thức A
b)tính giá trị biểu thức A biết 4a^2+b^2=5ab a>b>0
Cho a+b=1.Tính giá trị M=2a^3+2b^3-3(a^2+b^2)
Hộ mik nha!Thanks!
M = 2(a+b) ( a^2 - ab + b ^2) - 3( a^2 + b ^2)
= 2 (a^2 + b^2 ) - 2ab - 3(a^2 + b^2)
= - ( a^2+2ab+b^2) = - (a+b)^2 = -1
Chúc bạn học tốt!