giải phương trình nghiệm nguyên 3x2-2xy+y-5x+2=0

Những câu hỏi liên quan
giải phương trình nghiệm nguyên: 5x2+2xy+y2-4x-40 bằng 0
tìm nghiệm nguyên x,y của phương trình : 3x^2-2xy+y-5x+2=0
PT \(\Leftrightarrow\left(3x^2-5x\right)-2xy+\left(y+2\right)=0\)
Xét \(\Delta'=y^2-\left(y+2\right)\ge0\Leftrightarrow y^2-y-2\ge0\)
\(\Leftrightarrow-y^2+y+2\le0\Leftrightarrow\left(y-2\right)\left(y+1\right)\)
\(\Leftrightarrow-1\le y\le2\)
Thế vô làm tiếp :v
Đúng 0
Bình luận (0)
tìm nghiệm nguyên x,y của phương trình : 3x^2-2xy+y-5x+2=0
giải phương trình nghiệm nguyên:
\(3x^2-2xy+y-5x+2=0\)
mong các bạn giúp mình
học lớp 6 thôi,sai thôi nhé
Ta có (1-2x)y=-32+5x-2
Do x nguyên nên 1-2x khác 0
=>y=\(\frac{3x^2-5x+2}{2x-1}\)<=>4y=\(\frac{12x^2-20x+8}{2x-1}\)=6x-7+\(\frac{1}{2x-1}\)
Do x,y là số nguyên =>\(\frac{1}{2x-1}\)là số nguyên,nên 2x-1 thuộc (1;-1).Từ đó tìm đc (x;y) là (1;0),(0;-2)
Đúng 0
Bình luận (0)
bạn giải ra cho mình nhé, tại mình có biết làm đâu
giải đúng tất nhiên là phải tích rồi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giai phương trình nghiệm nguyên : 3x^2-2xy+y-5x+2=0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
3x2 + 5x + 2 = 0
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
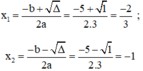
Vậy phương trình có hai nghiệm là -1 và 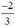
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình:
4x2-2xy+5x+y+1=0.
hình như sai đề bạn. chỉ có x hoặc y thôi chứ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình nghiệm nguyên :
a) \(2x^4-2x^2y+y^2-64=0\)
b) \(5x^2+2y^2+2xy+3y-4=0\)
\(2x^4-2x^2y+y^2-64=0.\)
\(x^4+x^4-2x^2y+y^2-64=0.\)
\(\left(x^4-2x^2y+y^2\right)+x^4-64=0.\)
\(\left(x^2-y\right)^2+x^4-64=0.\)
\(\left(x^2-y\right)^2+x^4=64.\)
Có \(\left(x^2-y\right)^2\ge0\)
mafk \(\left(x^2-y\right)^2+x^4=64.\)
\(\Rightarrow x^4\le64.\)
\(\Rightarrow x^2\le8\)
Từ đó xét tiếp
Đúng 0
Bình luận (0)
Giải nghiệm nguyên của phương trình :
\( x^2+2xy+y^2+x+4y=0\)

















