Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
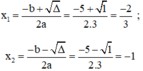
Vậy phương trình có hai nghiệm là -1 và 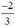
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
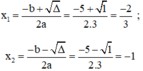
Vậy phương trình có hai nghiệm là -1 và 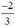
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a ) 2 x 2 − 7 x + 3 = 0 b ) 6 x 2 + x + 5 = 0 c ) 6 x 2 + x − 5 = 0 d ) 3 x 2 + 5 x + 2 = 0 e ) y 2 − 8 y + 16 = 0 f ) 16 z 2 + 24 z + 9 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
y2 – 8y + 16 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
6x2 + x + 5 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
2x2 – 7x + 3 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
6x2 + x – 5 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
16z2 + 24z + 9 = 0
Cho phương trình: 3x2 – 5x – 6 = 0 có 2 nghiệm x1, x2. Không giải phương trình, hãy tính giá trị của biểu thức sau : 
cho phương trình : x^2 + 5x - 1 = 0 ( 1 )
Không giải phương trình ( 1 ), hãy lập 1 phương trình bậc hai có các nghiệm là lũy thừa bậc bốn của các nghiệm của phương trình ( 1 )
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0