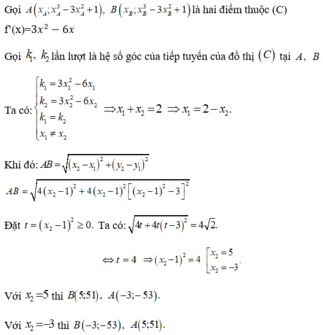Cho hàm số y=-3x2 tìm trên đồ thị hàm số 2 điểm A và B sao cho cùng tung độ và khoảng cách AB=12

Những câu hỏi liên quan
Cho hàm số y = 4x.
a) Điểm A(2; 4) có thuộc đồ thị hàm số trên không? Vì sao?
b) Tìm tọa độ điểm B, biết B thuộc đồ thị hàm số trên và B có tung độ là 4.
\(a.\)\(Thay:A\left(2,4\right)\) vào hàm số :
\(\Rightarrow2\cdot4\ne4\)
\(\Rightarrow A\notin y=4x\)
\(b.\\ B\left(x,4\right)\)
\(\Rightarrow4=4x\)
\(\Rightarrow x=1\)
\(B\left(1,4\right)\)
Đúng 1
Bình luận (0)
a) Thay x=2 vào hàm số y=4x, ta được:
\(y=4\cdot2=8\ne y_A\)
Vậy: Điểm A(2;4) không thuộc đồ thị hàm số
b) Vì điểm B thuộc đồ thị hàm số y=4x và B có tung độ bằng 4 nên Thay y=4 vào hàm số y=4x, ta được:
4x=4
hay x=1
Vậy: B(1;4)
Đúng 0
Bình luận (0)
Cho điểm A( 2;-1) thuộc đồ thị hàm số y = ax.
a) Xác định a.
b) Tìm điểm B có hoành độ là 2 và điểm C có tung độ bằng 5 thuộc đồ thị hàm số y = ax.
c) Vẽ đồ thị hàm số y =ax vừa tìm được và đồ thị hàm số y = 2x trên cùng một hệ trục tọa
độ Oxy.
d) Chứng minh 3 điểm M(-3; 1,5); N (1; -0,5) và O thẳng hàng.
LẸ GIÙM MÌNH NHA
a: Thay x=2 và y=-1 vào y=ax, ta được:
2a=-1
hay a=-1/2
Đúng 0
Bình luận (0)
a) Vẽ đồ thị hàm số y = 3x.
b) Tìm toạ độ điểm A, biết A thuộc đồ thị hàm số trên và A có tung độ là 6.
c) Tìm điểm trên đồ thị sao cho điểm đó có tung độ và hoành độ bằng nhau.
b) Vì A(xA;yA) có tung độ bằng 6 nên yA=6
Thay y=6 vào hàm số y=3x, ta được:
\(3\cdot x=6\)
hay x=2
Vậy: A(2;6)
c) Gọi điểm có tung độ và hoành độ bằng nhau trên đồ thị hàm số y=3x là B(xB;yB)
nên xB=yB
Thay x=y vào hàm số y=3x, ta được:
y=3y
\(\Leftrightarrow y=0\)
Vậy: Điểm trên đồ thị hàm số y=3x có tung độ và hoành độ bằng nhau có tọa độ là (0;0)
Đúng 3
Bình luận (0)
Cho hàm số: `y=x^2` và `y=-x+2`
`a,` Tìm tọa độ giao điểm của đồ thị `2` hàm số trên và tọa độ tung điểm `I` của đoạn thẳng `AB` biết điểm `A` có hoành độ dương
`b,` Tìm tọa độ điểm `M in (P): y =x^2` sao cho `ΔAMB` cân
\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{46}\\ =1-\dfrac{1}{46}\\ =\dfrac{45}{46}\\ \Rightarrow S< 1\)
Đúng 0
Bình luận (0)
Gọi ` ƯCLN(n+1 ; 2n+3)=d`
Ta có:
`n+1 vdots d => 2n+2 vdots d`
`2n+3 vdots d`
`=>(2n+3)-(2n+2) vdots d`
`=>2n+3-2n-2 vdots d`
`=>1 vdots d`
`=>ƯCLN(n+1; 2n+3)=1`
`=> (n+1)/(2n+3)` tối giản
Đúng 0
Bình luận (0)
Gọi ` ƯCLN(2n+1,3n+4)=d`
Ta có:
`2n+1 vdots d => 6n+3 vdots d`
`3n +4 vdots d =>6n+8 vdots d`
`=>(6n+8)-(6n+3) vdots d`
`=>6n+8-6n-3 vdots d`
`=>5 vdots d`
Giả sử phân số rút gọn được
`=>2n+1 vdots 5`
`=>2n+1+5 vdots 5`
`=>2n+6 vdots 5`
`=>2(n+3) vdots 5`
`=>n+3 vdots 5`
`=>n = 5k-3`
`=> n ne 5k-3`
Vậy để phân số trên tối giản thì ` n ne 5k-3`
Đúng 0
Bình luận (0)
Bài 1: Cho hàm số yax^2a) Xác định a biết đồ thị của hàm số đi qua A(3;3)b) Vẽ đồ thị hàm số vừa tìm được ở câu ac) Tìm điểm thuộc đồ thị có tung độ bằng 1Bài 2: Cho hai hàm số: yx^2 (P) và y2x (d)a) vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độb) Tìm tọa độ gioa điểm của (P) và (d)Bài 3: Cho hai hàm số y (m+1)x^2 và y 2x-1.Tìm m biết rằng đồ thị của hai hàm số cắt nhau tại điểm có hoành độ bằng 2
Đọc tiếp
Bài 1: Cho hàm số y=ax^2
a) Xác định a biết đồ thị của hàm số đi qua A(3;3)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tìm điểm thuộc đồ thị có tung độ bằng 1
Bài 2: Cho hai hàm số: y=x^2 (P) và y=2x (d)
a) vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độ
b) Tìm tọa độ gioa điểm của (P) và (d)
Bài 3: Cho hai hàm số y= (m+1)x^2 và y= 2x-1.
Tìm m biết rằng đồ thị của hai hàm số cắt nhau tại điểm có hoành độ bằng 2
Bài 3:
a/ Trong mặt phẳng Oxy, vẽ đồ thị hàm số y = - 3x.
b/ Điểm A(2 ; 6) có thuộc đồ thị hàm số trên không? Vì sao?
c/ Tìm tọa độ điểm B, biết B thuộc đồ thị hàm số trên và B có tung độ là 4.
b: Thay x=2 vào y=-3x, ta được:
\(y=-3\cdot2=-6< >y_A\)
Vậy: A không thuộc đồ thị hàm số y=-3x
c: Thay y=4 vào y=-3x, ta được:
-3x=4
hay y=-4/3
Đúng 0
Bình luận (0)
Cho hàm số y = x3 – 3x2 + 1 (C). Tìm tổng hoành độ của hai điểm A; B trên đồ thị hàm số sao cho tiếp tuyến của đồ thị (C) tại A; B song song với nhau và A B = 4 2
A: 1
B: 2
C: 3
D: 5
Bài 4. Cho các hàm số: y 3x và y -3x +41)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y -3x +4.4)Trong các điểm: C(dfrac{1}{3};3) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y -3x+4. Vì sao?5)Tìm trên đường thẳng y -3x+4 điểm có hoành độ bằng xdfrac{2}{3} .6) Tìm trên đường thẳng y -3x+4 điểm có tung độ bằng y -2 .7) Tìm trên đường thẳng y -3x +4 điể...
Đọc tiếp
Bài 4. Cho các hàm số: y =3x và y =-3x +4
1)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.
2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.
3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y =-3x +4.
4)Trong các điểm: C(\(\dfrac{1}{3};3\)) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y= -3x+4. Vì sao?
5)Tìm trên đường thẳng y =-3x+4 điểm có hoành độ bằng x=\(\dfrac{2}{3}\) .
6) Tìm trên đường thẳng y =-3x+4 điểm có tung độ bằng y = -2 .
7) Tìm trên đường thẳng y =-3x +4 điểm M (x;y) sao cho y2+ xy -2x2=0.
8) Tìm trên đường thẳng y =-3x+4 điểm N(x;y) sao cho khoảng cách từ N đến Ox bằng 4 lần khoảng cách từ N đến Oy
Bài tập Cho hàm số y=x-5 có đồ thị (d1) và hàm số y=-2x+1 có đồ thị (d2) a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ b) tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán c) tính khoảng cách từ O đến đường thẳng (d1), khoảng cách từ O đến đường thẳng (d2)
a: 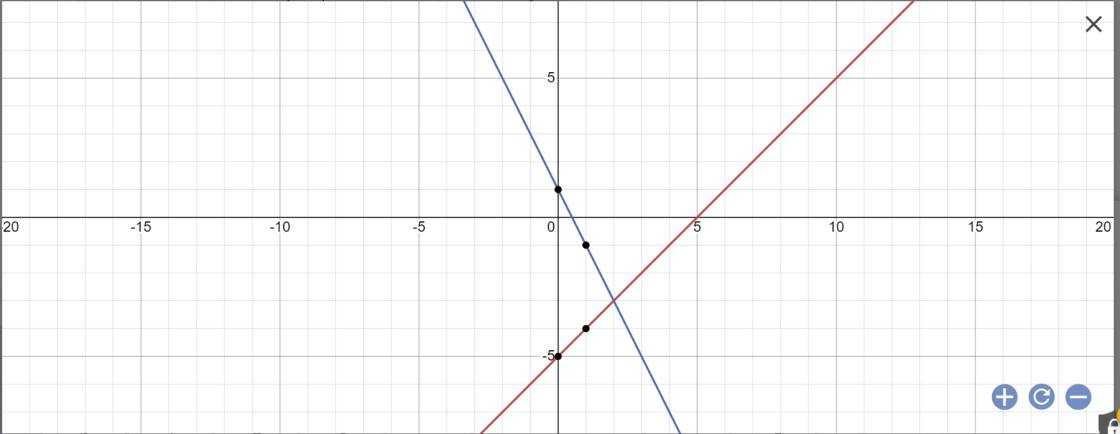
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)
Đúng 2
Bình luận (0)