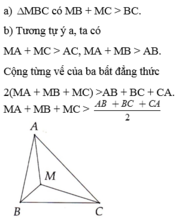
cho tam giác abc va điểm m nằm trong tam giác. CMR MB+MC<AB+AC

Những câu hỏi liên quan
Cho tam giác ABC , điểm M nằm trong tam giác sao cho MB < MC . CMR : góc AMB > góc AMC
Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Đúng 0
Bình luận (0)
Cho điểm M nằm trong tam giác ABC. 1) So sánh AB với MA + MB . 2) CMR: AB + AC + BC < 2(MA + MB + MC) . 3) Chứng minh rằng MA + MB +MC lớn hơn nửa chu vi tam giác ABC.
Cho tam giác ABC , M là một điểm nằm trong tam giác
a) cmr: MB+MC<AB+AC
b) P<MA+MB+MC<2P
cho tam giác ABC và điểm M nằm trong tam giác CMR : 1/2 AB+AC+BC<MA+MB+MC<AB+AC+BC
CHo tam giác ABC điểm M nằm trong tam giác . C/M
a) MB+ MC < AB +AC
b) C/M MA+MB+MC< chu vi tam giác ABC
cho tam giác ABC , M nằm trong tam giác ABC . MB cắt AC tại D
CMR :
a, MB+MC < DB+DC
b, MB+MC <AB +AC
c , MB+MC+MA <AM+BC+AC
dùng bất đẳng thức tam giác!!!!!!!!
758769
Đúng 0
Bình luận (0)
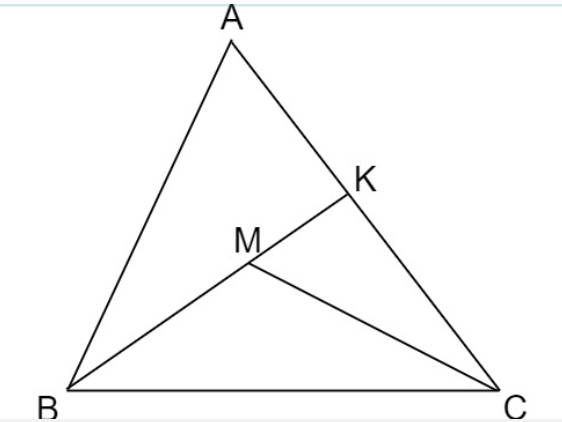
Cho tam giác ABC, điểm M nằm trong tam giác. Chứng minh: MB+MC < AB+AC
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)
Đúng 3
Bình luận (1)
Cho tam giác ABC, M là một điểm nằm trong tam giác. Gọi D, E, F, H, I, K là trung điểm của MA, MB, MC, BC, CA và AB. CMR: DH, EI,FK đồng quy
tứ giác AEBD và ABDF là hình bình hành vì có các cạnh đối song song
do đó,AE = BD va AF=BD
=> AE =AF
Lại có AE //BD ,AF //BD nên 3 điểm A,E,F thẳng hàng .Từ đó ta có A là trung điểm của EF .
tương tự B là trung điểm của EC ;D là trung điểm của CF
CA,FB,CD là các đường trung tuyến của tam giác ECF nên chúng đồng quy.
Đúng 2
Bình luận (0)
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.a) So sánh MB + MC với BCb) Chứng minh
M
A
+
M
B
+
M
C
A
B
+
B
C
+
C
A
2
Đọc tiếp
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2