Bài 7 (2) :Cho hình thang ABCD (AB//CD) ; hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N . Chứng minh OM = ON
Bài 7. Cho hình thang ABCD, đáy AB = 40cm, CD = 80cm, BC = 50cm, AD = 30cm. Chứng minh rằng ABCD là hình thang vuông.
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2
=> 502= 30^2 +40^2
=> 50^2 = 2500
=> 50^2 = 50^2
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2AG2=AD2+DG2
⇒502=302+402⇒502=302+402
⇒502=900+1600
⇒502=2500
⇒502=502
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
hơi dài nha![]()
Bài 2. Cho hình thang ABCD (AB // CD) có AB=1cm, CD = 5cm và C = 30°, D = 60°. Tính diện tích hình thang ABCD.
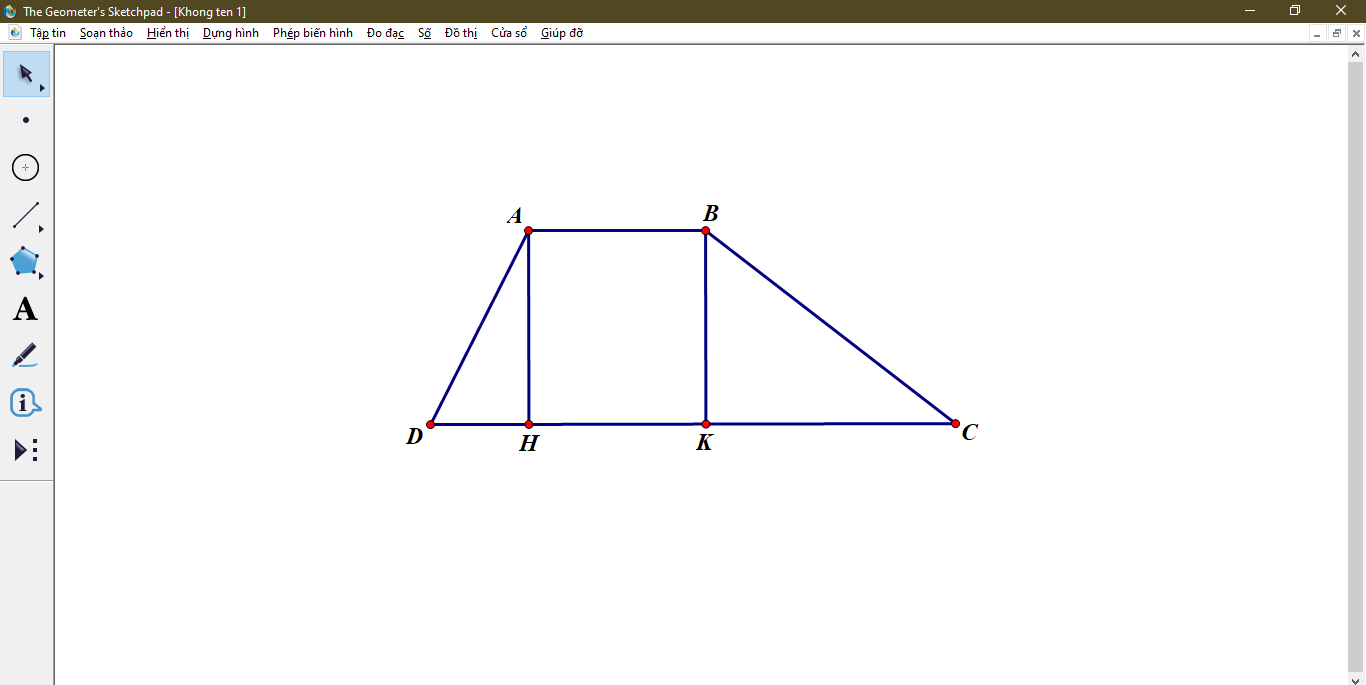
Kẻ đường cao AH và đường cao BK . ⇒AB=HK=1cm
Nên ta có : DH+CK=4 (1)
Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có :
\(\left\{{}\begin{matrix}AH=tan60\cdot DH\\BK=tan30\cdot CK\end{matrix}\right.\)\(\Rightarrow tan60\cdot DH=tan30\cdot CK\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}DK+CK=4\\\sqrt{3}DH-\dfrac{\sqrt{3}}{3}CK=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DH=1\\CK=3\end{matrix}\right.\)
\(\Rightarrow AH=tan60\cdot DH=\sqrt{3}\cdot1=\sqrt{3}\left(cm\right)\)
Tick hộ nha bạn 😘
BÀI 2; Cho hình cân ABCD ( AB // CD ) ; góc A = 120 độ. Tính các góc còn lại của hình thang.
BÀI 3; Cho hình thang cân ABCD ( AB // CD );
BÀI 2; Cho hình cân ABCD ( AB // CD ) ; góc A = 120 độ. Tính các góc còn lại của hình thang.
Giải:
Xét hình thang cân ABCD ta có:
góc BAD + góc ADC = 180 độ ( 2 góc trong cùng phía bù nhau do AB//CD)
=> 120 độ + góc ADC = 180 độ
=> góc ADC = 60 dộ
Vì tiws giác ABCD là hình thang cân
=> góc BAD = góc ABC = 120 độ
=> góc ADC = góc BCD = 60 độ
BÀI 3; Cho hình thang cân ABCD ( AB // CD ), có góc A = 2 góc C. Tính các góc của hình thang ABCD.
BÀI 4; Cho hình thang cân ABCD có AB // CD. Các đường thẳng chứa hai cạnh bên cắt nhau tại O. CM : OA = OB
Do AB // CD ( GT )
⇒^A+^C=180o
⇒2^C+^C=180o
⇒3^C=180o
⇒^C=60o
⇒ ^A = 60o * 2 = 120o
Do ABCD là hình thang cân
⇒ ^C = ^D
Mà ^C = 60o
⇒ ^D = 60o
AB // CD ⇒ ^D + ^B = 180o
⇒ˆB=180o − 60o = 120o
Vậy ^A = ^B = 120o ; ^C= ^D = 60o
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB : Cạnh chung
^DAB=^CBA (Tính chất của hình thang cân)
AC = BD ( Tính chất của hình thang cân)
⇒ ΔADB = ΔBCA ( c−g−c)
⇒ ^CAB = ^DBA (2 góc tương ứng)
⇒ ^OAB = ^OBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Bài 1. Cho hình thang cân ABCD (AB\\CD), A=3D. Tính các góc của hình thang cân.
Bài 2. Cho tam giác cân ABC cân tại A có BH và CK là hai đường cao của tam giác. Chứng minh BCHK là hình thang cân.
Bài 3.Cho hình thang cân ABCD (AB\\CD) có O là giao điểm hai đường chéo. Chứng minh OA = OB, OC = OD.
Bài 4.Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy điểm M, N sao cho BM = CN.
a) Chứng minh BMNC là hình thang cân.
b) Tính các góc tứ giác BMNC biết góc A=400
Bài 5. Cho hình thang cân ABCD (AB\\CD) có AB=8cm, BC=AD=5cm, CD=14cm. Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Chứng minh: CD-AB=2AK. Từ đó tính độ dài BH.
c) Tính diện tích hình thang ABCD.
Bài 6. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc BCD.
Bài 6:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Bài 1. Cho hình thang cân ABCD (AB\\CD), A=3D. Tính các góc của hình thang cân.
Bài 2. Cho tam giác cân ABC cân tại A có BH và CK là hai đường cao của tam giác. Chứng minh BCHK là hình thang cân.
Bài 3.Cho hình thang cân ABCD (AB\\CD) có O là giao điểm hai đường chéo. Chứng minh OA = OB, OC = OD.
Bài 4.Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy điểm M, N sao cho BM = CN.
a) Chứng minh BMNC là hình thang cân.
b) Tính các góc tứ giác BMNC biết góc A=400
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK và HB=KC
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{HC}\)
Do đó: KH//BC
Xét tứ gác BKHC có KH//BC
nên BKHC là hình thang
mà KC=BH
nên BKHC là hình thang cân
Bài 1. Cho hình thang cân ABCD (AB\\CD), A=3D. Tính các góc của hình thang cân.
Bài 2. Cho tam giác cân ABC cân tại A có BH và CK là hai đường cao của tam giác. Chứng minh BCHK là hình thang cân.
Bài 3.Cho hình thang cân ABCD (AB\\CD) có O là giao điểm hai đường chéo. Chứng minh OA = OB, OC = OD.
Bài 4.Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy điểm M, N sao cho BM = CN.
a) Chứng minh BMNC là hình thang cân.
b) Tính các góc tứ giác BMNC biết góc A=400
Bài 5. Cho hình thang cân ABCD (AB\\CD) có AB=8cm, BC=AD=5cm, CD=14cm. Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Chứng minh: CD-AB=2AK. Từ đó tính độ dài BH.
c) Tính diện tích hình thang ABCD.
Bài 6. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc BCD.
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
Do đó: HK//BC
Xét tứ giác BCHK có HK//BC
nên BCHK là hình thang
mà HB=KC(ΔAHB=ΔAKC)
nên BCHK là hình thang cân
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
giải hộ 2 bài này với , mắc khó luôn :
Cho hình thang ABCD có đáy AB = 1/3 CD . Biết diện tích hình tam giác ABC là 18cm2 . Tính diện tích hình thang ABCD
Cho hình thang ABCD có đáy AB = 2/3 CD . Biết diện tích hình tam giác ADC bằng 24cm2 . Tính diện tích hình thang ABCD
gọi BH,AH lần lượt là đường cao của tam giác ABC và hình thang ABCD (AH=BH)
ta có diện tích tam giác ABC= \(\frac{ABxBH}{2}\)=18cm2
mà AB=1/3CD suy ra CD=3AB
mà diện tích hình thang ABCD= \(\frac{CDxAH}{2}\)=\(\frac{3ABxAH}{2}\)=3x\(\frac{ABxAH}{2}\)= 18 x 3 = 36cm2 (AH=BH)