Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d khác O; các điểm A', B' thuộc (P) thỏa mãn \(AA' \bot (P),\,BB' \bot (P)\). Chứng minh rằng: \(\frac{{AA'}}{{BB'}} = \frac{{OA}}{{OB}}\)

Những câu hỏi liên quan
cho đường tròn (o) đường kính ab lấy 2 điểm c,d thuộc (o) ( c và d thuộc 2 nửa mặt phẳng khác nhau có bờ là ab ). kẻ tiếp tuyến b cắt nhau tại đường thẳng ac,ad lần lượt tại e và f. a) chứng minh dcef nội tiếp
góc ACB=góc ADB=1/2*180=90 độ
=>BC vuông góc AE và BD vuông góc AF
ΔABE vuông tại B có BC là đường cao
nên AC*AE=AB^2
ΔABF vuông tại B có BDlà đường cao
nên AD*AF=AB^2
=>AC*AE=AD*AF
=>AC/AF=AD/AE
=>ΔACD đồng dạng vớiΔAFE
=>góc ACD=góc AFE
=>góc DCE+góc DFE=180 độ
=>DCEF nội tiếp
Đúng 0
Bình luận (0)
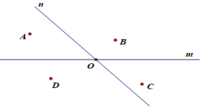
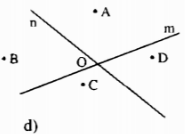
Vẽ hình theo các bước diễn đạt sau:- Hai đường thẳng m và n cắt nhau tại điểm O.- Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m.- Hai điểm A, B nằm cùng phía đối với đường thẳng m nhưng khác phía đối với đường thẳng n.- Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A.- Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m.
Đọc tiếp
Vẽ hình theo các bước diễn đạt sau:
- Hai đường thẳng m và n cắt nhau tại điểm O.
- Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m.
- Hai điểm A, B nằm cùng phía đối với đường thẳng m nhưng khác phía đối với đường thẳng n.
- Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A.
- Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m.
Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19).
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
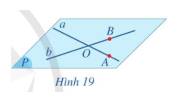
a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b
b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b
Đúng 0
Bình luận (0)
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng (a , b) tại I khác O . Gọi M là điểm di động trên c và khác I . Chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên một mặt phẳng cố định .
*Tìm giao tuyến của 2 mặt phẳng (M,a) và (M,b):
Có M là một điểm chung
Theo bài : a và b cắt nhau tại O
=> O thuộc a ⊂ (M,a) =>O thuộc (M,a)
và O thuộc b ⊂ (M,b) =>O thuộc (M,b)
=>O là điểm chung thứ hai
Vậy: (M,a) ∩ (M,b) = OM
Do đó giao tuyến OM lun thuộc mặt phẳng tạo bởi c và O ( mp (O,c)) là một mp cố định.
Đúng 0
Bình luận (0)
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng(a , b) tại điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên 1 mặt phẳng cố định .
cho 2 đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mặt phẳng(a , b) tại điểm I khác O . Gọi M là điểm di động trên C và khác I . chứng minh rằng giao tuyến của các mặt phẳng (M , a) , (M , b) nằm trên 1 mặt phẳng cố định .
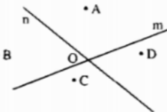
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp dưới đây. Hai đường thẳng m và n cắt nhau tại điểm O. Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m. Hai điểm A, B ở cùng phía với đường thẳng m nhưng khác phía đối với đường thẳng n. Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A. Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m.
Đọc tiếp
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp dưới đây. Hai đường thẳng m và n cắt nhau tại điểm O. Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m. Hai điểm A, B ở cùng phía với đường thẳng m nhưng khác phía đối với đường thẳng n. Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A. Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m.
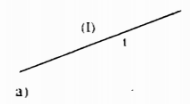
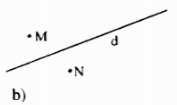
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây :
a) Nửa mặt phẳng (I) có bờ là đường thẳng t.
b) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng d và điểm N thuộc nửa mặt phẳng đối
c) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng a. Hai điểm M, N nằm khác phía đối với đường thẳng a. Hai điểm N, P nằm khác phía đối với đường thẳng a
d) Hai đường thẳng m và n cắt nhau tại điểm O. Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m. Hai điểm A, B ở cùng phía với đường thẳng m như...
Đọc tiếp
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây :
a) Nửa mặt phẳng (I) có bờ là đường thẳng t.
b) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng d và điểm N thuộc nửa mặt phẳng đối
c) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng a. Hai điểm M, N nằm khác phía đối với đường thẳng a. Hai điểm N, P nằm khác phía đối với đường thẳng a
d) Hai đường thẳng m và n cắt nhau tại điểm O. Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m. Hai điểm A, B ở cùng phía với đường thẳng m nhưng khác phía đối với đường thẳng n. Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A. Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m
Cho hai đường tròn (O;R) và (O';R') cắt nhau tại A, B (O và O' thuộc hai nửa mặt phẳng bờ AB). Các đường thẳng AO và AO' cắt
(O) tại hai điểm C,D và cắt đường tròn (O') tại E, F. Chứng minh:
a) Ba điểm C,B,F thẳng hàng
b) Tứ giác CDEF nội tiếp.