Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình vuông.
Các mệnh đề sau đúng hay sai?
a) \(C \subset D\);
b) \(C \supset D\);
c) \(C = D\).
Câu 13: Chọn câu đúng A. Hình bình hành có hai đường chéo vuông góc là hình vuông B. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông C. Hình bình hành có hai đường chéo vuông góc là hình chữ nhật D. Hình bình hành có một góc vuông là hình chữ nhật Câu 14: Chọn câu sai A. Hình bình hành có hai đường chéo vuông góc là hình thoi B. Hình chữ nhật có hai đường chéo vuông góc là hình vuông C. Tứ giác có hai cạnh đối bằng nhau là hình bình hành D. Hình bình hành có hai cạnh kề bằng nhau là hình thoi
Câu 13: Chọn câu đúng
A. Hình bình hành có hai đường chéo vuông góc là hình vuông B. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
C. Hình bình hành có hai đường chéo vuông góc là hình chữ nhật
D. Hình bình hành có một góc vuông là hình chữ nhật
Câu 14: Chọn câu sai
A. Hình bình hành có hai đường chéo vuông góc là hình thoi
B. Hình chữ nhật có hai đường chéo vuông góc là hình vuông
C. Tứ giác có hai cạnh đối bằng nhau là hình bình hành
D. Hình bình hành có hai cạnh kề bằng nhau là hình thoi
Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ”, phát biểu lại các định lí sau:
a) Nếu \(B \subset A\) thì \(A \cup B = A\) (A, B là hai tập hợp);
b) Nếu hình bình hành ABCD có hai đường chéo vuông góc với nhau thì nó là hình thoi.
a) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:
P: “\(B \subset A\)” và Q: “\(A \cup B = A\)”. Có thể phát biểu dưới dạng:
\(B \subset A\) là điều kiện đủ để có \(A \cup B = A\)
\(A \cup B = A\) là điều kiện cần để có \(B \subset A\)
b) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:
P: “Hình bình hành ABCD có hai đường chéo vuông góc với nhau” và Q: “ABCD là hình thoi”. Có thể phát biểu dưới dạng:
Hình bình hành ABCD có hai đường chéo vuông góc với nhau là điều kiện đủ để ABCD là hình thoi.
ABCD là hình thoi là điều kiện cần để có ABCD là hình bình hành có hai đường chéo vuông góc với nhau.
Chọn câu đúng trong các câu sau :
A/ Hình thoi có hai đường chéo vuông góc với nhau và bằng nhau.
B/ Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.
C/ Hình bình hành có đường chéo là đường phân giác các cặp góc đối là hình thoi.
D/ Tứ giác có các cạnh đối bằng nhau là hình thoi.
Hình nào sau đây là hình thoi ? A. Hình bình hành có hai đường chéo bằng nhau B. Tứ giác có hai cạnh kề bằng nhau C. Tứ giác có một đường chéo là phân giác của một góc D. Hình bình hành có hai đường chéo vuông góc
Trong các phát biểu sau
a. Trực tâm là giao điểm của ba đường phân giác.
b. Hình bình hành có hai đường chéo bằng nhau.
c. Hình thoi có hai đường chéo vuông góc.
d. Trọng tâm là giao điểm của ba đường trung tuyến.
e. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các phát biểu đúng là:
A. b, c, d
B. c, d, e
C. a, c, d, e
D. c, d
Đáp án: B
a sai vì trực tâm là giao điểm của ba đường cao, không phải ba đường phân giác.
b sai vì hai đường chéo của hình bình hành không bằng nhau.
c, d, e đúng.
Chọn câu trả lời đúng
Tứ giác có hai đường chéo vuông góc là hình thoi
Hình thoi là tứ giác có tất cả các góc bằng nhau
Hình bình hành có một đường chéo là đường phân giác của một góc là hình vuông
Hình chữ nhật có hai đường chéo vuông góc là hình vuông
Một mảnh vườn hình vuông có chu vi là 28m. Diện tích của mảnh vườn đó là
49cm²
56m²
784m²
49m²
Rút gọn biểu thức M = x³ – 8 – (x – 1)(x² + x + 1), ta được
2x³– 9
2x³ – 7
– 7
– 9
Xóa lựa chọn
13cm
7,5cm
6,5cm
10cm
Khi x = –2 thì A = 5
Khi x = 1 thì A = 8
Khi x = –1 thì A có giá trị nhỏ nhất bằng 4
A có luôn có giá trị âm
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF = A C 2
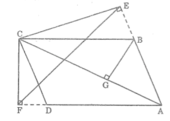
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: 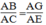
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: 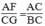 ⇒ BC.AF = AC.CG
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2
Bài tập: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C kẻ đường vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB, AD). Chứng minh: AB . AE + AD . AF = AC2
- Bài này khó, bạn làm biết làm thì giúp mình nhé. Cám ơn nhìu!
Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
a) Hình thang có hai góc vuông là hình chữ nhật.
b) Hình thang cân có một góc vuông là hình chữ nhật.
c) Hình bình hành có một góc vuông là hình chữ nhật.
d) Hình bình hành có hai đường chéo cắt nhau trại trung điểm mỗi đường là hình chữ nhật.
Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
`a)` Hình thang có hai góc vuông là hình chữ nhật.
`->` Sai
`->` Hình thang có hai cạnh góc vuông là hình chữ nhật .
`b)` Hình thang cân có một góc vuông là hình chữ nhật.
`->` Đúng
`c)` Hình bình hành có một góc vuông là hình chữ nhật.
`->` Đúng
`d)` Hình bình hành có hai đường chéo cắt nhau trại trung điểm mỗi đường là hình chữ nhật.
`->` Sai
`->` Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật .