Cho hàm số y=ax2 +bx+3:
Lập bảng biến thiên và vẽ đồ thị hàm số trên khi a=1;b=4
Cho hàm số y = x 3 + a x 2 + bx+1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b
Với a = 1; b = -1, hàm số trở thành: y = x 3 + x 2 – x + 1.
- Tập xác định : D = R.
- Sự biến thiên :
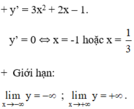
+ Bảng biến thiên :
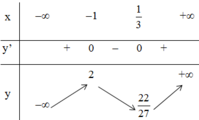
Kết luận :
Hàm số đồng biến trên (-∞ ; -1) và 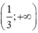
Hàm số nghịch biến trên 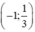
Hàm số đạt cực đại tại x = -1 ; yCĐ = 2.
Hàm số đạt cực tiểu tại 
- Đồ thị :
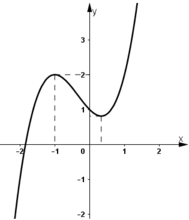
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên.
y = ax + b
y = a x 2 + b x + c
* Hàm số y = ax + b
Trường hợp a > 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ R.
QUẢNG CÁO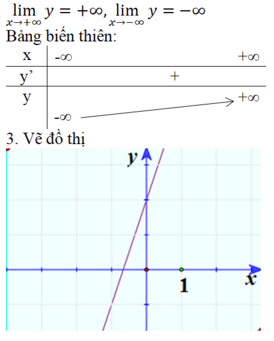
Trường hợp a < 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ R.
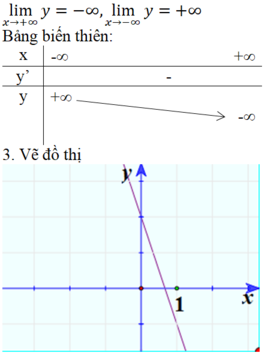
* Hàm số y = ax2 + bx + c
Trường hợp a > 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
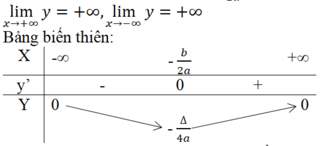
Hàm số nghịch biến trên khoảng (-∞,- b/2a).
Hàm số đồng biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực tiểu bằng - Δ/4a tại x = - b/2a .
3. Vẽ đồ thị:
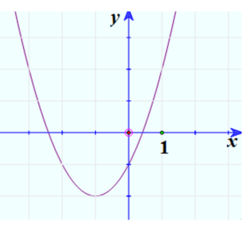
Trường hợp a < 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
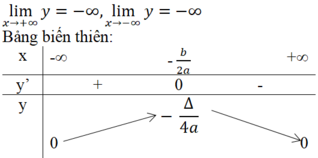
Hàm số đồng biến trên khoảng (-∞,- b/2a).
Hàm số nghịch biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực đại bằng - Δ/4a tại x = - b/2a .
3. Vẽ đồ thị:
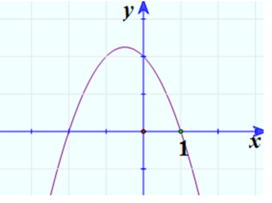
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
Cho (P) : y=ax2+bx+c đi qua điểm F(0;5) và coa đỉnh I(3:-4)
a) xác định (P)
b) Khảo sát số biến thiên và vẽ đồ thị hàm số (P) vừa tìm được
a.
Do (P) đi qua F, thay tọa độ F vào phương trình (P) ta được:
\(a.0^2+b.0+c=5\Rightarrow c=5\)
Do (P) có đỉnh \(I\left(3;-4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=3\\a.3^2+b.3+c=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3b+5=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3.\left(-6a\right)=-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)
hay pt (P) có dạng: \(y=x^2-6x+5\)
b. Em tự giải
Cho hàm số y = a - 1 x 3 3 + ax 2 + 3 a - 2 x
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với a = 3/2.
Từ đó suy ra đồ thị của hàm số
y = x 3 6 + 3 x 2 2 + 5 x 2
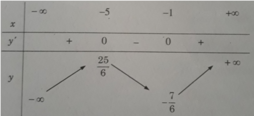
Khi a = 3/2 thì
![]()
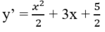
y' = 0 ⇔ x 2 + 6x + 5 = 0 ⇔ x = -1 hoặc x = -5.
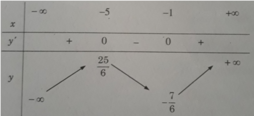
Đồ thị như trên Hình 1.18
Vì
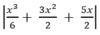
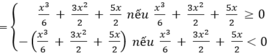
nên từ đồ thị (C) ta suy ngay ra đồ thị của hàm số
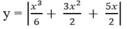
như trên Hình 1.19
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2
Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.
Vậy:
+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)
+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)
+ f(x) = 0 nếu x = -2 hoặc x = 1.
b)
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:
+ Tập xác định: D = R
+ Đỉnh I1( -1; -2)
+ Trục đối xứng: x = -1
+ Giao điểm với trục tung tại gốc tọa độ.
+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).
+ Bảng biến thiên:
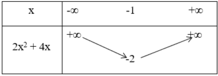
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:
+ Tập xác định D = R.
+ Đỉnh 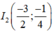
+ Trục đối xứng: x = -3/2
+ Giao với trục tung tại D(0; 2)
+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)
+ Bảng biến thiên
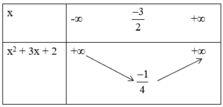
* Đồ thị:
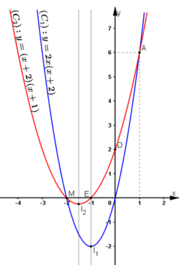
* Tìm tọa độ giao điểm:
Cách 1: Dựa vào đồ thị hàm số:
Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)
Cách 2: Tính:
Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:
2x(x + 2) = (x + 2)(x + 1)
⇔ (x + 2).2x – (x + 2)(x + 1) = 0
⇔ (x + 2).(2x – x – 1) = 0
⇔ (x + 2).(x – 1) = 0
⇔ x = -2 hoặc x = 1.
+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)
+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).
c)
+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)
⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c
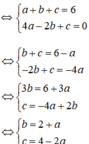
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:
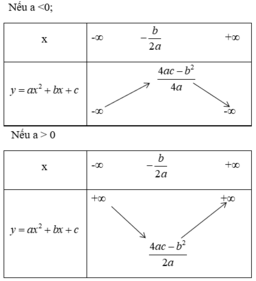
Nhận thấy y đạt giá trị lớn nhất bằng 8
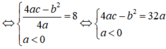
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:
4.a.(4 – 2a) – (2 + a)2 = 32a
⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a
⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0
⇔ -9a2 - 20a - 4 = 0
⇔ a = -2 hoặc a = -2/9.
Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8
Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số 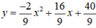
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)
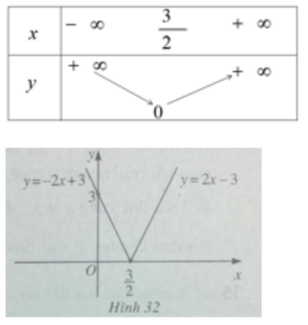
Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số
y = | 2 x - 3 |
Ta có thể viết

Từ đó có bảng biến thiên và đồ thị của hàm số
y = |2x - 3| (h.32)