Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H∈BC). Chứng minh rằng:
a) HB = HC;
b) BAH=CAH
Những câu hỏi liên quan
Cho tam giác ABC cân tại A . Kẻ AH vuông tại góc với BC ( H thuộc BC )
Chứng minh HB = HC
tham khảo
a/ xét 2 tam giác vuông ABH và ACH,có:
AB=AC(gt),AH chung =>tam giác vuông ABH=tam giác vuông ACH
=>HB=HC(t/ứng
Đúng 0
Bình luận (0)
Xét 2 tam giác vuông ABH và ACH,có: AB=AC(gt),AH chung =>tam giác vuông ABH=tam giác vuông ACH =>HB=HC
Đúng 0
Bình luận (0)
Vì tg ABC cân tại A.
=>AB=AC.
Xét tg AHC và tg AHB, có:
AH chung.
góc AHB= góc AHC(=90o)
AB=AC(cmt)
=>tg AHB= tgAHC(ch-cgv)
=>HB=HC(2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng:a) HBHCb) góc BAH góc CAKBài 2: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng: tam giác ABM tam giác DCMBài 3: Cho tam giác ABC vuông ở A. Trên tia đối AC lấy điểm D sao cho AD ACa) chứng minh: tam giác ABC tam giác ABDb) Trên tia đối của tia AB lấy điểm M. Chứng minh: tam giác MBD tam giác MBC
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng:
a) HB=HC
b) góc BAH= góc CAK
Bài 2: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng: tam giác ABM= tam giác DCM
Bài 3: Cho tam giác ABC vuông ở A. Trên tia đối AC lấy điểm D sao cho AD= AC
a) chứng minh: tam giác ABC= tam giác ABD
b) Trên tia đối của tia AB lấy điểm M. Chứng minh: tam giác MBD= tam giác MBC
3:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
AB chung
AC=AD
=>ΔABC=ΔABD
b: Xét ΔCBM và ΔDBM có
BM chung
góc CBM=góc DBM
BC=BD
=>ΔCBM=ΔDBM
Đúng 1
Bình luận (1)
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.a)Chứng minh: ΔAHB ΔAHC.b)Chứng minh: HB HC và góc BAH góc CAHc)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I. Chứng minh: ΔHKB ΔHIC.Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.Kẻ DK⊥AB tại K.a)Chứng minh ΔABDΔKBD.b)Tia KD cắt tia BA tại M. Chứng minh AMKC và ΔBMC cân.c)Chứng minh AK // MC.Chứng minh BD⊥MC.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
a)Chứng minh: ΔAHB = ΔAHC.
b)Chứng minh: HB = HC và góc BAH = góc CAH
c)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I.
Chứng minh: ΔHKB = ΔHIC.
Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.
Kẻ DK⊥AB tại K.
a)Chứng minh ΔABD=ΔKBD.
b)Tia KD cắt tia BA tại M. Chứng minh AM=KC và ΔBMC cân.
c)Chứng minh AK // MC.
Chứng minh BD⊥MC.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABH=ΔACH
nên HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC
Đúng 0
Bình luận (0)
Câu 8 Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H BC) a) Chứng minh HB HC b) Chứng minh góc BAH góc CAH c) Kẻ HD vuông góc với AB (D thuộc AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân
Đọc tiếp
Câu 8 Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H 
BC)
a) Chứng minh HB = HC
b) Chứng minh góc BAH =góc CAH
c) Kẻ HD vuông góc với AB (D thuộc AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A , kẻ AH vuông góc với BC ( H thuộc BC)
a)chứng minh HB =HC
b)kẻ HD vuông góc với AB ( D thuộc AB) và HE vuông góc với AC ( E thuộc AC) . Chứng minh tam giác HDE cân
cho tam giác cân ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh rằng:
a) HB = HC
b) góc BAH = góc CAH
hình bạn tự vẽ
a/ xét 2 tam giác vuông ABH và ACH,có:
AB=AC(gt),AH chung =>tam giác vuông ABH=tam giác vuông ACH
=>HB=HC(t/ứng)
b/ Vì tam giác vuông BAH=tam giác vuông ACH(cmt) =>\(\widehat{BAH}\)=\(\widehat{CAH}\)(t/ứng)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A Kẻ AH vuông góc với BC H thuộc BC a chứng minh HB = HC B Tính độ dài cạnh A2 cho biết AB = 10 cm BC = 12 cm ơ c kẻ HD vuông góc với AB D thuộc AB AC AD vuông góc với AC E thuộc AC Chứng minh tam giác hde cân D nếu cho góc Bac bằng 120 độ thì tam giác AC d e trở thành tam giác gì Vì sao
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng
HB = HC
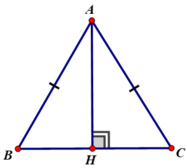
Xét hai tam giác vuông ΔABH và ΔACH đều vuông tại H có:
AB = AC (gt)
AH cạnh chung
Nên ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)
Suy ra HB = HC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc với BC ( H thuộc BC )
a) Chứng minh: HB = HC và góc BAH = góc CAH
c) Kẻ HD vuông góc với AB tại D, HE vuông góc với AC tại E. Chứng minh tam giác HDE cân.
cho tam giác abc cân tại a có AB=AC=5cm, BC=8cm. kẻ AH vuông góc với BC (H thuộc BC) a) chứng minh HB=HC và góc BAH= góc CAH. b) tính độ dài AH. c) kẻ HD vươong góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H
Đúng 3
Bình luận (1)