Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Xét các số thực với a ≠ 0 , b > 0 sao cho phương trình a x 3 - x 2 + b = 0 có ít nhất hai nghiệm thực. Giá trị lớn nhất của biểu thức a 2 b bằng
A. 4 27 .
B. 15 4 .
C. 27 4 .
D. 4 15 .
Xét các số thực với a ≠ 0 , b > 0 sao cho phương trình a x 3 - x 2 + b = 0 có ít nhất hai nghiệm thực. Giá trị lớn nhất của biểu thức a 2 b bằng
A. 4 27
B. 15 4
C. 27 4
D. 4 15
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Cho a, b là các số thực thỏa mãn a > 0 v à a ≠ 1 biết phương trình a x - 1 a x = 2 c o s ( b x ) có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình a 2 x - 2 a x ( c o s b x + 2 ) + 1 = 0
A. 14
B. 0
C. 7
D. 28
Nếu a, b, c, d là các số thực khác 0, biết c và d là nghiệm của phương trình x 2 + a x + b = 0 và a, b là nghiệm của phương trình x 2 + c x + d = 0 thì
A. -2
B. 0
C. − 1 + 5 2
D. 2
c và d là nghiệm của phương trình:
x 2 + a x + b ⇒ ⇒ c + d = − a ( 1 ) c d = b ( 2 )
a, b là nghiệm của phương trình:
x 2 + c x + d = 0 ⇒ ⇒ a + b = − c ( 3 ) a b = d ( 4 )

Đáp án cần chọn là: A
Cho a, b, c ∈R,a ≠ 0, z 1 , z 2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình a x 2 +bx+c=0. Hãy tính z 1 + z 2 và z 1 . z 2 theo hệ số a, b, c.
Cách 1 :
Phương trình a z 2 + bz + c = 0 có Δ = b 2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức 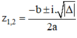
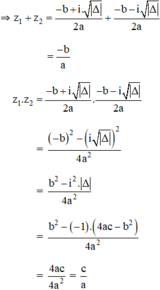
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
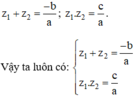
Cách 2 :

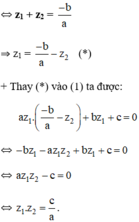
xét các số thực a,b,c (a≠0) sao cho phương trình ax2+bx+c=0 có 2 nghiệm m, n thỏa mãn \(0\le m\le1;0\le m\le1\). tìm GTNN của \(Q=\dfrac{2a^2-ac-2ab+bc}{a^2-ab+ac}\)
\(Q=\dfrac{2-\dfrac{c}{a}-\dfrac{2b}{a}+\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)}{1-\dfrac{b}{a}+\dfrac{c}{a}}=\dfrac{2-mn+2\left(m+n\right)-mn\left(m+n\right)}{1+m+n+mn}\)
\(Q=\dfrac{\left(2-mn\right)\left(m+n+1\right)}{\left(m+1\right)\left(n+1\right)}\ge\dfrac{\left[8-\left(m+n\right)^2\right]\left(m+n+1\right)}{\left(m+n+2\right)^2}\)
Đặt \(m+n=t\Rightarrow0\le t\le2\)
\(Q\ge\dfrac{\left(8-t^2\right)\left(t+1\right)}{\left(t+2\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{\left(2-t\right)\left(4t^2+15t+10\right)}{4\left(t+2\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(t=2\) hay \(m=n=1\)
Xét các phương trình bậc 2 \(ax^2+bx+c=0\) với các hệ số a, b, c là những số nguyên dương không vượt quá 100. Hỏi số các phương trình có nghiệm và các phương trình vô nghiệm, số nào lớn hơn ?