Cho dãy số (Un) xác định bởi: { U1=1; Un+1=1/2un + 3/2; ∀n ϵ N*
Tình giới hạn của dãy số (Un)
Ai đó giúp em với, em cảm ơn rất nhiều ạ
Những câu hỏi liên quan
Cho dãy số
u
n
được xác định bởi
u
1
2
u
n
+
1...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
1) cho dãy số (un)(��) được xác định bởi unn^2-1�3�−1a) Tính u1,u2,u3,u4b) 99 là số hạng thứ mấy của dãy2) cho dãy số (un)(��) được xác định bởi u_ndfrac{2n-1}{n+1}a) Tính u1,u2,u3,u4b) dfrac{13}{7} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
5
và
u
n
+
1
3
+
u
n
. Số hạng tổng quát của dãy số này là: A.
u
n
8
+
n
B.
u
n...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 5 và u n + 1 = 3 + u n . Số hạng tổng quát của dãy số này là:
A. u n = 8 + n
B. u n = 2 + 3 n
C. u n = 5 + 3 n
D. u n = 5 . 3 n
Chọn B.
- Ta có, u 1 = 5 và u n + 1 = 3 + u n nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu u 1 = 5 .
- Do đó số hạng tổng quát của dãy số này là:
Đúng 0
Bình luận (0)
Cho dãy số
U
n
xác định bởi
U
1
1
3
và
U
n
+
1
n
+
1
3
n...
Đọc tiếp
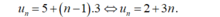
Cho dãy số U n xác định bởi U 1 = 1 3 và U n + 1 = n + 1 3 n U n . Tổng S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Cho dãy số
u
n
xác định bởi:
u
1
1
3
;
u
n
+
1
n
+
1
3
n
u
n
. Tổng
S
u
1
+
u...
Đọc tiếp
Cho dãy số u n xác định bởi: u 1 = 1 3 ; u n + 1 = n + 1 3 n u n . Tổng S = u 1 + u 2 2 + u 3 3 + . . . + u 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Dãy số
(
u
n
)
xác định bởi
u
1
2
u
n
+
1...
Đọc tiếp
Dãy số ( u n ) xác định bởi u 1 = 2 u n + 1 = u n + 1 2 là dãy
A. Giảm và bị chặn dưới
B. Giảm và không bị chặn dưới
C. Tăng và không bị chặn trên
D. Tăng và bị chặn dưới
Dãy số (un) xác định bởi
u
1
2
u
n
+
1
u
n...
Đọc tiếp
Dãy số (un) xác định bởi u 1 = 2 u n + 1 = u n + 1 2 là dãy
A. Giảm và bị chặn dưới
B. Giảm và không bị chặn dưới
C. Tăng và không bị chặn trên
D. Tăng và bị chặn dưới
Cho dãy số
U
n
xác định bởi
U
1
1
3
và
U
n
+
1
n
+
1
3
n
U
n
.
Tổng...
Đọc tiếp
Cho dãy số U n xác định bởi U 1 = 1 3 và U n + 1 = n + 1 3 n U n . Tổng S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Đáp án B
U 2 = 2 3 . 1 U 1 , U 3 = 3 3 . 2 . 2 3 . 1 U 1 , . . . , U 10 = 10 3 . 9 . 9 3 . 8 . . . 2 3 . 1 U 1 ⇒ S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 = U 1 + U 1 3 + U 1 3 3 + . . . + U 1 3 9 = U 1 1 - 1 3 10 1 - 1 3 = 29524 59049
Đúng 0
Bình luận (0)
Cho dãy số (Un) xác định bởi
u
1
1
3
và
u
n
+
1
n
+
1
3
n
.
u
n
. Tổng
S
u
1
+...
Đọc tiếp
Cho dãy số (Un) xác định bởi u 1 = 1 3 và u n + 1 = n + 1 3 n . u n . Tổng S = u 1 + u 2 2 + u 3 3 + . . . . . + u 10 10 bằng
Chọn B.
Đặt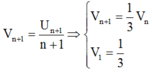 
suy ra 
trong đó Vn là cấp số nhân với công sai q = 1/3
Do đó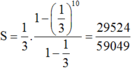 
Đúng 0
Bình luận (0)
Cho dãy số
U
n
xác định bởi
U
1
1
3
và
U
n
+
1
n
+
1
3
n
U...
Đọc tiếp
Cho dãy số U n xác định bởi U 1 = 1 3 và U n + 1 = n + 1 3 n U n . Tổng S = U 1 + U 2 2 + U 3 3 + ... + U 10 10 bằng:
A. 3280 6561 .
B. 29524 59049 .
C. 25942 59049 .
D. 1 243 .
