Cho nửa (O;R) đường kính AB lấy một điểm C cố định (C≠A và B) và một điểm M bất kì trên cung nhỏ AC.Kẻ MH⊥AB tại H,gọi K là giao điểm của AC và MH , E là giao điểm của MB và AC.Chứng minh AM2=AK.AC
Em cần gấp ạ
Những câu hỏi liên quan
1 tháng 12 2023 lúc 12:49
Bài 5: Cho nửa đường tròn tâm O, đường kính AB. Vẽ 2 tiếp tuyến Ax, By của nửa (O). Gọi C là điểm trên nửa (O) sao cho AC > BC. Tiếp tuyến tại C của nửa (O) cắt Ax và By lần lượt ở D và E.
a) Cm ∆ABC vuông và AD + BE = ED.
b) Cm 4 điểm A, D, C, O cùng thuộc 1 đường tròn và góc ADO = góc CAB.
c) DB cắt nửa (O) tại F và cắt AE tại I. Tia CI cắt AB tại K. Cm IC = IK.
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
Xét (O) có
DC,DA là tiếp tuyến
Do đó: DC=DA
Xét (O)có
EC,EB là tiếp tuyến
Do đó: EC=EB
DC+CE=DE
mà DC=DA và EC=EB
nên DA+EB=DE
b: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}=90^0+90^0=180^0\)
=>DAOC là tứ giác nội tiếp
=>D,A,O,C cùng thuộc một đường tròn
Xét ΔOAC có OA=OC=R
nên ΔOAC cân tại O
ADCO là tứ giác nội tiếp
=>\(\widehat{ADO}=\widehat{ACO}\)
mà \(\widehat{ACO}=\widehat{OAC}\)(ΔOAC cân tại O)
nên \(\widehat{ADO}=\widehat{OAC}=\widehat{CAB}\)
Đúng 3
Bình luận (0)
cho nửa (o) đường kính ab. lấy c trên nửa (o) sao cho ac=r. gọi k là giao điểm của tiếp tuyến tại a với nửa (o) và đường thẳng bc. từ k kẻ tiếp tuyến thứ 2 vuông góc với nửa (o) tại m. ok cắt am tại e. cminh kc*kb=oe*ok
Cho nửa đường tròn (O;R) đường kính AB. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (O;R) vẽ các tiếp tuyến Ax, By với nửa đường tròn (O;R).Gọi M là 1 điểm bất kì trên nửa đường tròn (O;R) ,(M≠A;M≠B) Tiếp tuyến của nửa đường tròn tại M cắt Ax,By lần lượt tại C và Da) Chứng minh tứ giác ACMO nội tiếp , tứ giác OMDN nội tiếp b) Chứng minh AC.BDR²c) Kẻ MN vuông góc AB (N thuộc AB) ; BC cắt MN tại I . Chứng minh I là trung điểm của MN
Đọc tiếp
Cho nửa đường tròn (O;R) đường kính AB. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (O;R) vẽ các tiếp tuyến Ax, By với nửa đường tròn (O;R).Gọi M là 1 điểm bất kì trên nửa đường tròn (O;R) ,(M≠A;M≠B) Tiếp tuyến của nửa đường tròn tại M cắt Ax,By lần lượt tại C và D
a) Chứng minh tứ giác ACMO nội tiếp , tứ giác OMDN nội tiếp
b) Chứng minh AC.BD=R²
c) Kẻ MN vuông góc AB (N thuộc AB) ; BC cắt MN tại I . Chứng minh I là trung điểm của MN
a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
góc DMO+góc DBO=180 độ
=>DMOB nội tiếp
b: Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc DOC=1/2*180=90 độ
Xét ΔDOC vuông tại O có OM là đường cao
nên CM*MD=OM^2
=>AC*BD=R^2
Đúng 0
Bình luận (0)
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a.
Do AD là tiếp tuyến tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D thuộc đường tròn đường kính OD (1)
BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (2)
(1);(2) \(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc đường tròn đường kính OD
b.
Do D là giao điểm 2 tiếp tuyến tại A và B, theo t/c hai tiếp tuyến cắt nhau
\(\Rightarrow DA=DB\)
Mà \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB \(\Rightarrow OD\perp AB\) (3)
BC là đường kính và A thuộc đường tròn nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow BA\perp CA\) (4)
(3);(4) \(\Rightarrow OD||CA\) (cùng vuông góc AB) hay \(OD||CE\)
Áp dụng hệ thức lượng trong tam giác vuông BCE với đường cao BA ứng với cạnh huyền:
\(BC^2=CA.CE\Rightarrow\left(2R\right)^2=CA.CE\)
\(\Rightarrow CA.CE=4R^2\)
Đúng 1
Bình luận (2)
Em kiểm tra lại đề bài, đoạn này là sao nhỉ: "Tiếp tuyến tại 4 của (O) "
Đúng 0
Bình luận (4)
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a: Xét tứ giác ADBO có
\(\widehat{DBO}+\widehat{DAO}=90^0+90^0=180^0\)
=>ADBO là tứ giác nội tiếp
=>A,D,B,O cùng thuộc một đường tròn
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)AC tại A
=>BA\(\perp\)CE tại A
Xét (O) có
DA,DB là các tiếp tuyến
DO đó: DA=DB
=>D nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OD là đường trung trực của AB
=>OD\(\perp\)AB
Ta có: OD\(\perp\)AB
CE\(\perp\)AB
Do đó: OD//CE
Xét ΔEBC vuông tại B có BA là đường cao
nên \(CA\cdot CE=CB^2\)
=>\(CA\cdot CE=\left(2R\right)^2=4R^2\)
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB.trong cùng nửa mặt phẳng bờ AB với nửa đường tròn (O),vẽ nửa đường tròn tâm O , đường kính OA.trên OB lấy điểm H sao cho OH1/3 OB,đường vuông góc với AB tại H cắt nửa đường tròn tâm O tại C,AC cắt nửa đường tròn tâm O tại điểm thứ 2 là D a) CM: DADCb) CM rằng tiếp tuyến tại D của (O) và tiếp tuyến tại C của (O) song song vs nhauc) CM tiep tuyen tại D của (O) đi qua B
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB.trong cùng nửa mặt phẳng bờ AB với nửa đường tròn (O),vẽ nửa đường tròn tâm O' , đường kính OA.trên OB lấy điểm H sao cho OH=1/3 OB,đường vuông góc với AB tại H cắt nửa đường tròn tâm O tại C,AC cắt nửa đường tròn tâm O' tại điểm thứ 2 là D
a) CM: DA=DC
b) CM rằng tiếp tuyến tại D của (O') và tiếp tuyến tại C của (O) song song vs nhau
c) CM tiep tuyen tại D của (O') đi qua B
24 tháng 1 2022 lúc 20:41
Cho nửa đường tròn (O) đường kính AB . Lấy M là điểm tùy ý (HvarepsilonAB) . Trên cùng nửa mawtjj phẳng bờ AB chứa nửa đường tròn (O) vẽ hai đường tròn tâm O_1, đường kính AH và tâm O_2,đường kính BH , MA và MB cắt hai nửa đường tròn (O_1)và (O_2) lần lượt tại P và Q. Chứng minh:a) MHPQb) Các tam giác MPQ và tam giác MBA đồng dạng;c) PQ là tiếp tuyến chung của hai đường tròn (O_1) và (O_2).
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB . Lấy M là điểm tùy ý (H\(\varepsilon\)AB) . Trên cùng nửa mawtjj phẳng bờ AB chứa nửa đường tròn (O) vẽ hai đường tròn tâm O\(_1\), đường kính AH và tâm O\(_2\),đường kính BH , MA và MB cắt hai nửa đường tròn (O\(_1\))và (O\(_2\)) lần lượt tại P và Q. Chứng minh:
a) MH=PQ
b) Các tam giác MPQ và tam giác MBA đồng dạng;
c) PQ là tiếp tuyến chung của hai đường tròn (O\(_1\)) và (O\(_2\)).
Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn. Vẽ tiếp tuyến Ax với nửa (O). Lấy điểm C trên nửa đường tròn, BC cắt Ax tại D.a) C/m AD^2DB.DC b) Gọi E là trung điểm của AD. C/m EC là tiếp tuyến của nửa (O)c) Kẻ CHperp AB tại H, CH cắt BE tại I, AC cắt OE tại F. C/m IFperp AD
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn. Vẽ tiếp tuyến Ax với nửa (O). Lấy điểm C trên nửa đường tròn, BC cắt Ax tại D.
a) C/m \(AD^2=DB.DC\)
b) Gọi E là trung điểm của AD. C/m EC là tiếp tuyến của nửa (O)
c) Kẻ \(CH\perp AB\) tại H, CH cắt BE tại I, AC cắt OE tại F. C/m \(IF\perp AD\)
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABD vuông tại A có AC là đường cao
nên \(AD^2=DB\cdot DC\)
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C Da chứng minh AC + BD CD và tam giác BCD vuông tại Ob Tính tích AC nhân BD theo ABc các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Đọc tiếp
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C D
a chứng minh AC + BD = CD và tam giác BCD vuông tại O
b Tính tích AC nhân BD theo AB
c các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
Đọc tiếp
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.
a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.
b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
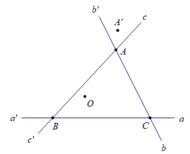
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.
Đúng 0
Bình luận (0)