Question

Cho nửa (O;R) đường kính AB lấy một điểm C cố định (C≠A và B) và một điểm M bất kì trên cung nhỏ AC.Kẻ MH⊥AB tại H,gọi K là giao điểm của AC và MH , E là giao điểm của MB và AC.Chứng minh AM²=AK.AC

Em cần gấp ạ

Answer 1

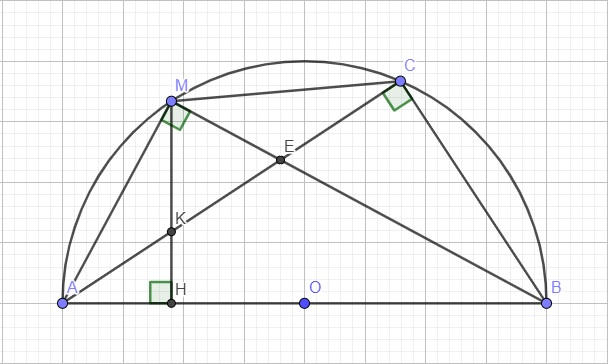
ABCM nội tiếp (cùng thuộc đường tròn đường kính AB) 

\(\Rightarrow\widehat{ABM}=\widehat{ACM}\) (cùng chắn AM)

Lại có \(\widehat{ABM}=\widehat{AMH}\) (cùng phụ \(\widehat{BAM}\))

\(\Rightarrow\widehat{ACM}=\widehat{AMH}\)

Xét hai tam giác AMK và ACM có:

\(\left\{{}\begin{matrix}\widehat{AMH}=\widehat{ACM}\left(cmt\right)\\\widehat{MAC}\text{ chung}\end{matrix}\right.\)  \(\Rightarrow\Delta AMK\sim\Delta ACM\left(g.g\right)\)

\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AK}{AM}\Rightarrow AM^2=AK.AC\)

Answer 2