tam giác ABC cân tại A vẽ đường tròn (O;R) tiếp xúc AB ,AC tại B , C . Đường thẳng qua điểm M trên BC vuông góc với OM cắt tia AB, AC tại D,E
a, CM 4 điểm O,B,D,M thuộc1 đg tròn
b, CM MD=ME
HELP
cho tam giác ABC cân tại A nội tiếp đường tròn (O). vẽ trung tuyến AM của tam giác ABC. gọi B' đối xứng với B qua O .Vẽ qua A vuông góc với CB' và cắt BC' tại H chứng minh AH là tiếp tuyến của đường tròn (O)
Cho đường tròn tâm O, tam giác ABC cân tại A nội tiếp đường tròn tâm O. Vẽ đường thẳng đi qua A cắt BC tại D và đường tròn tâm O tại E. CMR: AB^2= AE.AD
Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng: Điểm E nằm trên đường tròn (O).
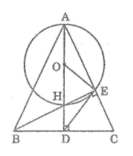
Gọi O là trung điểm của AH
Tam giác AEH vuông tại E có EO là đường trung tuyến nên :
EO = OA = OH = AH/2 (tính chất tam giác vuông)
Vậy điểm E nằm trên đường tròn (O ; AH/2 )
Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng: DE là tiếp tuyến của đường tròn (O).
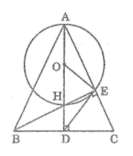
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
![]()
Trong tam giác BDH ta có:
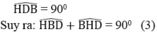
Từ (1), (2) và (3) suy ra:
![]()
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
![]()
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).
giúp tui câu này đc ko chiều tui thi r cho tam giác ABC cân tại A nội tiếp đường tròn (O). vẽ trung tuyến AM của tam giác ABC. gọi B' đối xứng với B qua O .Vẽ qua A vuông góc với CB' và cắt BC' tại H chứng minh AH là tiếp tuyến của đường tròn (O)
Cho tam giác abc cân tại A nội tiếp đường tròn (O;R). Vẽ đường tròn (O;R1)(với R1<R) cắt cạnh AB,AC lần lượt tại E,F và M,N.Cmr MN=EF
Cho đường tròn tâm O ngoại tiếp tam giác ABC cân tại A qua A vẽ 1 cắt tuyến cắt dây BC tại D và cắt đường tròn tâm O tại E Chứng minh rằng AB^2 = AD × AE
Cho đường tròn (O) và 1 điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B, C là các tiếp điểm). AO cắt BC tại D
a/ Chứng minh tam giác ABC cân tại A và AO là đường trung trực của BC
b/ Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh tam giác AGO đồng dạng tam giác HDO
c/ Chứng minh EH là tiếp tuyến của đường tròn (O)

câu c thì cơ bản là tui chứng minh hai tam giác bằng nhau (c-c-c), xong rồi tui suy ra hai góc bằng nhau
Cho đường tròn (O) và 1 điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B, C là các tiếp điểm). AO cắt BC tại D
a/ Chứng minh tam giác ABC cân tại A và AO là đường trung trực của BC
b/ Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh tam giác AGO đồng dạng tam giác HDO
c/ Chứng minh EH là tiếp tuyến của đường tròn (O)
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>ΔABC cân tại A
mà OB=OC
nên OA là trung trực của BC
b: ΔOEF cân tại O
mà OG là trung tuyến
nên OG vuông góc với EF
Xét ΔAGO vuông tại G và ΔHDO vuông tại D có
góc AOG chung
Do đó: ΔAGO đồng dạng với ΔHDO
c: ΔAGO đồng dạng vơi ΔHDO
=>OA/OH=OG/OD
=>OA*OD=OH*OG
=>OH*OG=OE^2
=>ΔHEO vuông tại E
=>HE là tiếp tuyên của (O)
cho tam cân ABC ( cân tại A). GỌi O là trung điểm của BC. Vẽ đường tròn tâm O, bán kính OB, đường tròn này cắt AB,AC lần lượt ở M,N. CMR:
a) BM=CM
b) Tam giác OBM= tam giác OCN
c) Góc NBA=1/2 góc MON
d) AO,CM, BN đồng quy
a)Sửa đề: BM=CN
Xét (O) có
OB là bán kính(gt)
O là trung điểm của BC(gt)
Do đó: BC là đường kính của (O)
Xét (O) có
ΔBMC nội tiếp đường tròn(B,M,C∈(O))
BC là đường kính của (O)(cmt)
Do đó: ΔBMC vuông tại M(Định lí)
Xét (O) có
ΔBNC nội tiếp đường tròn(B,N,C∈(O))
BC là đường kính của (O)(cmt)
Do đó: ΔBNC vuông tại N(Định lí)
Xét ΔBMC vuông tại M và ΔCNB vuông tại N có
BC là cạnh chung
\(\widehat{MBC}=\widehat{NCB}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBMC=ΔCNB(cạnh huyền-góc nhọn)
⇒BM=CN(hai cạnh tương ứng)
b) Xét ΔOBM và ΔOCN có
OB=OC(=R)
OM=ON(=R)
BM=CN(cmt)
Do đó: ΔOBM=ΔOCN(c-c-c)
Lời giải:
a) Đề đúng phải là CMR $BM=CN$.
Xét tam giác $BMC$ và $CNB$ có:
$\widehat{BMC}=\widehat{CNB}=90^0$ (góc nt chắn nửa đường tròn)
$\widehat{B}=\widehat{C}$ (do $ABC$ là tam giác cân tại $A$)
$\Rightarrow \triangle BMC\sim \triangle CNB$ (g.g)
$\Rightarrow BM=CN$ (đpcm)
b)
Xét tam giác $OBM$ và $OCN$ có:
$OB=OC=R$
$OM=ON=R$
$BM=CN$ (theo phần a)
$\Rightarrow \triangle OBM=\triangle OCN$ (c.c.c)
c)
$\widehat{NBA}=\widehat{NBM}=\frac{1}{2}\text{số đo cung MN}$
$\widehat{MON}=\text{số đo cung MN}$
$\Rightarrow \widehat{NBA}=\frac{1}{2}\widehat{MON}$
d)
$\widehat{BMC}=\widehat{CNB}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow BN\perp AC, CM\perp AB$
$ABC$ là tam giác cân tại $A$, $O$ là trung điểm $BC$ nên đường trung tuyến $AO$ đồng thời là đường cao. Suy ra $AO\perp BC$
Như vậy $AO, BN, CM$ là 3 đường cao của tam giác $ABC$ nên $AO, BN, CM$ đồng quy (đpcm)