Cho tam giác ABC vuông tại A. Đường tròn (O;R), đường kính AB cắt BC tại D. Tiếp tuyến của (O) tại D cắt AC ở P.
a.cm: tứ giác AODP nội tiếp
b.cm : tam giác PDC cân
c. khi góc ACB= 30, tính diện tích giới hạn bởi PA, PD và cung nhỏ AD của (O) theo R
Cho tam giác ABC vuông tại A. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, dlaf tiếp tuyến của đường tròn tại A. Các tiếp tuyến của đường tròn tại B và C cắt d tại D và E. Chứng minh góc DOE vuông
Gọi M là trung điểm DE. Khi đó MO là đường TB của hình thang BCED => MO vg với BC
Mà M là tâm đường tròn đường kính DE => DE là tiếp tuyến ...
Cho tam giác ABC vuông tại A, đường cao AH. Dựng đường tròn tâm O đường kính AB. Cho biết số đo góc ABC = 60 độ và AB = a . Tính theo a diện tích phần tam giác. ABC nằm ngoài đường tròn (O)
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
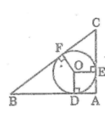
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
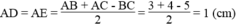
cho tam giác ABC vuông tại A, đường tròn tâm (O) đường kính AC cắt BC tại K, vẽ dây cung AD của đường tròn tâm (O) vuông góc với BO tại H
cho tam giác ABC nhọn nội tiếp đường tròn O ,2 đường cao BD và CE của tam giác ABC giao nhau tại H . kẻ đường kính AK của đường tròn O . KH cắt đường tròn O tại N
A/chứng minh năm diểm A,N,E,H.D cùng thuộc 1 đường tròn
B/ chứng minh AK vuông góc ED
C/ AN cắt BC tại Q , chứng minh 3 điểm Q,E,D thẳng hàng
thank UwU
a) Ta có: \(\angle AEH+\angle ADH=90+90=180\Rightarrow AEHD\) nội tiếp (1)
Vì AK là đường kính \(\Rightarrow\angle ANK=90\)
\(\Rightarrow\angle ANH+\angle ADH=90+90=180\Rightarrow ANHD\) nội tiếp (2)
Từ (1) và (2) \(\Rightarrow A,N,E,H,D\) cùng thuộc 1 đường tròn
b) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp
\(\Rightarrow\angle ADE=\angle ABC\)
Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle ADE+\angle OAC=90\Rightarrow AO\bot DE\)
c) DE cắt BC tại Q'.Q'A cắt (O) tại N'
Xét \(\Delta Q'EB\) và \(\Delta Q'CD:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'EB=\angle Q'CD\\\angle CQ'Dchung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'EB\sim\Delta Q'CD\left(g-g\right)\Rightarrow\dfrac{Q'E}{Q'C}=\dfrac{Q'B}{Q'D}\Rightarrow Q'B.Q'C=Q'D.Q'E\)
Xét \(\Delta Q'N'B\) và \(\Delta Q'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'N'B=\angle Q'CA\\\angle CQ'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'N'B\sim\Delta Q'CA\left(g-g\right)\Rightarrow\dfrac{Q'N'}{Q'C}=\dfrac{Q'B}{Q'A}\Rightarrow Q'B.Q'C=Q'N'.Q'A\)
\(\Rightarrow Q'N'.Q'A=Q'D.Q'E\Rightarrow AN'DE\) nội tiếp
mà AEHD nội tiếp \(\Rightarrow A,N',D,E,H\) cùng thuộc 1 đường tròn
\(\Rightarrow N\equiv N'\Rightarrow Q\equiv Q'\Rightarrow\) đpcm
cho đường tròn O đường kính AA'=2R.một dây cung BC vuông góc bán kính OA' tại trung điểm H của OA' a)chứng minh rằng tam giác OBA' và tam giác ABC là các tam giác đều.Tính cạnh tam giác ABC b)đường BO cắt đường tròn O tại D đường DH cắt đường tròn tại M.Tính DH;DM c)tính diện tích tam giác HMC
a:
góc ABA'=góc ACA'=1/2*180=90 độ
Xét ΔBOA' có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBOA' cân tại B
mà OB=OA'
nên ΔBOA' đều
=>góc A'BH=30 độ
=>góc ABC=60 độ
Xét ΔACB có
AH vừa là đường cao, vừa là trung tuyến
góc ABC=60 độ
=>ΔACb đều
b: ΔOBA' đều có BH là đường cao
nên BH=OA'*căn 3/2=R*căn 3/2
=>CH=R*căn 3/2
=>BC=R*căn 3
=>DC=căn DB^2-BC^2=R
DH=căn DC^2+CH^2=R*căn 7/2
Cho tam giác vuông ABC vuông tại A. Đường tròn O đường kính AB cắt Bc tại D (D khác B). Tia phân giác góc ABC cắt đường tròn O tại M
gọi H là giao điểm của đường cao AD và tia phân giác BM
biết góc MAC=góc MBC và tứ giác MHDE là tứ giác nội tiếp
chứng minh tam giác ABE cân
Cho tam giác ABC vuông cân tại A, đường cao AH. Biết AB = 5cm, BC = 6cm. a/ Tính các góc và các cạnh còn lại của tam giác ABC. b/ Dựng đường tròn tâm (O) ngoại tiếp tam giác ABC, tính độ dài bán kính của đường tròn tâm O.![]()
Bài 1:Cho tam giác cân ABC,AB=AC=6cm,đường cao AH=5cm.Gọi O là đường tròn tam giác ABC
a)Vì sao điểm O nằm trên AH
b)Tính độ dài đường kính AD của đường tròn tâm O
Bài 2:Cho tam giác ABC vuông tại A,đường cao AH,biết AH=12cm,HB=18cm.Tính bán kính đường tròn tam giác ABC
Bài 6. (2,5 điểm) Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt BC tại H. Gọi I là trung điểm AH, BI cắt đường tròn (O) tại E. Tia AE cắt BC tại K. a) Chứng minh tam giác ABH vuông tại H và KI vuông góc với AB. b) Chứng minh: tan ABK . tan AKB = 2. c) Đường thẳng qua H và song song với AC cắt AK tại M. Chứng minh: MC là tiếp tuyến đường tròn ngoại tiếp Tam giác ABC.