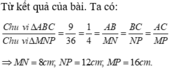Cho ▲ABC=▲MNP biết CA+BC=13cm;NP-MP=5Cm. Hỏi độ dài cạnh AC = bao nhiêu

Những câu hỏi liên quan
Cho tam giác ABC có cạnh AB = 2cm, BC = 3cm, CA = 4cm đồng dạng với tam giác MNP. Tính độ dài các cạnh của tam giác MNP biết chu vi của tam giác MNP là 36cm
Cho tam giác ABC có AB=2,BC=3,CA=4cm đồng dạng với tam giác MNP.Tính độ dài các cạnh của tam giác MNP biết chu vi MNP là 36
AB/MN=BC/NP=CA/PM=(AB+BC+CA)/(MN+NP+PM)=(2+3+4)/36=1/4
=> AB/MN=2/MN=1/4=> MN=8
Tương tự tính ra NP và PM
Tính chu vi của tam giác ABC là:9cm
Lấy chu vi tam giác MNP/tam giác ABC là: 36/9=4cm
=>MN=4.2=8(cm)
NP=4.3=12(cm)
MP=4.4=16(cm)
1)Cho △MNP có MN=6cm,MP=8cm,NP=10cm.Chứng minh △MNP vuông
2)Cho △ABC có AB=5cm,AC=13cm,BC=12cm.Chứng minh △ABC là tam giác vuông?
Nhớ trả lời cả 2 bài này nhé!
Bài 1:
Ta có: \(NP^2=10^2=100cm\)
\(MN^2+MP^2=6^2+8^2=100cm\)
Do đó: \(NP^2=MN^2+MP^2\)(=100cm)
Xét \(\Delta\)MNP có \(NP^2=MN^2+MP^2\)(cmt)
nên \(\Delta\)MNP vuông tại M(định lí pytago đảo)
Bài 2:
Ta có: \(AC^2=13^2=169cm\)
\(AB^2+BC^2=5^2+12^2=169cm\)
Do đó: \(AC^2=AB^2+BC^2\)(=169cm)
Xét \(\Delta\)ABC có \(AC^2=AB^2+BC^2\)(cmt)
nên \(\Delta\)ABC vuông tại B(định lí pytago đảo)
1) Xét ΔMNP ta có:
MN2 + MP2 = NP2 (vì 62 + 82 = 102)
=> ΔMNP vuông tại M
2) Xét ΔABC ta có:
AB2 + BC2 = AC2 (vì 52 + 122 = 132)
=> ΔABC vuông tại B
Cho tam giác ABC có BC = 13 cm, CA = 12 cm, AB = 5 cm. Biết tam giác ABC đồng dạng với tam giác MNP có cạnh nhỏ nhất là 2,5 cm. Tính độ dài các cạnh còn lại của tam giác MNP.
ΔABC đồng dạng với ΔMNP
=>\(\dfrac{AB}{MN}=\dfrac{BC}{NP}=\dfrac{AC}{MP}\)
ΔABC đồng dạng với ΔMNP
=>Độ dài cạnh nhỏ nhất của ΔMNP sẽ là độ dài tương ứng với cạnh nhỏ nhất của ΔABC
mà cạnh nhỏ nhất của ΔABC là AB và cạnh tương ứng của AB trong ΔMNP là MN
nên MN=2,5cm
=>\(\dfrac{5}{2,5}=\dfrac{12}{MP}=\dfrac{13}{NP}\)
=>\(\dfrac{12}{MP}=\dfrac{13}{NP}=2\)
=>MP=12/2=6(cm); NP=13/2=6,5(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC. M, N, P lần lượt là điểm chính giữa các cạnh BC, CA và AB. Tính diện
tích ABC biết diện tích MNP là 4,25cm2
Cho tam giác ABC, ba điểm M, N, P lần lượt thuộc BC, CA, AB sao cho BM/BC = CN/CA = AP/AB và BM/BC < 1/2. Chứng minh tam giác ABC và MNP có cùng trọng tâm
Cho tam giác ABC, gọi M,N,P theo thứ tự là trung điểm của AB, BC, CA. Tính cu vi của tam giác MNP biết AB =8cm , BC=12cm, AC=10cm
Cho tam giác ABC. Trên cạnh AB, BC, CA lấy M,N,P sao cho AM / MB = BN / NC = CP / PA = 1/2 .Tính S MNP biết S ABC = 27 cm ^
Mình cần cách giải chi tiết nhé
Cho tam giác ABC, M là trung điểm AB ; N là trung điểm BC; P) là trung điểm CA.
a) So sánh diện tích 4 hình tam giác AMP, MBN , PNC, MNP.
b) Tính diện tích hình tam giác MNP biết diện tích hình tam giác ABC là 600 cm vuông